Thermodynamique et mécanique des fluides appliquées aux

Lycée Newton - PT TMF - TD3 - Energétique des écoulements en conduite
Thermodynamique et mécanique des fluides
appliquées aux machines thermiques
TD no3 : Energétique des écoulements en conduite
Ex 1 Canalisation coudée
On consière une canalisation coudée de section Sconstante, formant un coude à angle droit, parcourue par un
écoulement d’eau à la vitesse v. On note Pla pression loin en amont du coude et ρla masse volumique de l’eau.
L’écoulement est stationnaire et supposé parfait. On néglige les effets de la pesanteur.
1.1. Déterminer la résultante (norme et direction) des actions de l’eau sur la partie coudée de la canalisation.
Ex 2 Vidange d’un récipient
On considère un récipient cylindrique de section horizontale Sinitialement rempli d’eau jusqu’à la hauteur h. En
bas du récipient, on perce un trou de section sS. L’écoulement est supposé parfait.
2.1. En précisant les approximations faites, déterminer la vitesse de l’eau à la sortie du récipient.
2.2. En déduire le temps nécessaire pour que le récipient se vide complètement.
Ex 3 Vase de Tantale
Un bassin rectangulaire est alimenté en permanence par de l’eau (fluide parfait incompressible, de masse volumique
ρ), avec un débit volumique entrant constant De. La surface totale du bassin est S=20 m2. Un siphon BC de diamètre
d=10 cm (section s) en assure la vidange. Il se termine en Cdonnant sur l’air libre, à l’extrémité d’un tronçon
horizontal dont l’axe est pris comme origine des cotes verticals. Le haut du siphon est à la cote h2=3 m. Le fond du
bassin est lui à la cote h0=1 m.
On donne ρ=1000 kg ·m−3;g=9,8 m ·s−2;PA=P0=1 bar la presseion atmosphrique.
Le siphon fonctionne de la façon suivante :
•il s’amorce dès que le niveau d’eau arrive à la hauteur h2=3 m ; l’écoulement de l’eau se produit alors et dure
tant que le siphon ne se désamorce pas ;
•dès que le niveau d’eau dans le bassin arrive à la hauteur h1=2 m, de l’air pénètre dans le siphon ; il se
désamorce et se vide alors complètement de toute l’eau qu’il contenait.
z
h2
z
h1
h0
•
A
•
B
•
C
De
Ds
On suppose le siphon initialement amorcé et z=h2.
3.1. Calculer le débit sortant initial Dsen Clorsque z=h2, puis discuter qualitativement de l’évolution du
système selon la valeur de De.
2015/2016 1/8

Lycée Newton - PT TMF - TD3 - Energétique des écoulements en conduite
3.2. On se place toujours dans le cas où le niveau initial est en h2; le débit d’netrée est fixé à De=30 L ·s−1. En
déduire la cote zmpour laquelle les deux débits Deet Dssont égaux. Conclure sur l’évolution de la cote zde la
surface libre de l’eau.
3.3. Quel temps t1met le plan d’eau pour atteindre sa cote minimale ?
On donne : Zdx
√x−a=2√x+2aln( √x−a)+cte
où a<√xest une constante.
3.4. Déterminer le temps t2de remontée de la surface libre jusqu’à l’état initial.
3.5. Déterminer la période des oscillations (dites de relaxation).
Ex 4 Sonde de Pitot
La figure ci-dessous montre une sonde de Pitot placé dans un écoulement d’air permanent et uniforme, à la vitesse
constante v=vex, loin en amont de la sonde. Deux trous sont percés dans la sonde : le trou Afait face à l’écoulement
et le trou Best sur le côté de la sonde.
•
A
•
B
sonde de Pitot
v
(a) Shéma d’une sonde de Pitot (b) Sonde de Pitot
Chaque trou mène sur une cavité bouchée, au fond de laquelle se trouve un capteur de pression.
4.1. En faisant les hypothèses simplificatrices nécessaires, montrer que la différence de pression PA−PBpermet
de connaître la norme de la vitesse vet donner l’expression de v.
4.2. Ces trous portent les noms de « prise de pression dynamique » et « prise de pression statique ». Expliquer
pourquoi.
4.3. En réalité, la masse volumique de l’air varie avec l’altitude et l’expression trouve à la question 4.1 n’est pas
exploitable directement. En assimilant l’air à un gaz parfait de masse molaire M, déterminer l’expression de la
vitesse ven fonction de la constante des gaz parfaits R, la température T,M,PAet PB.
4.4. Pourquoi les sondes de Pitot sont-elles indispensables dans un avion ?
Ex 5 Effet Venturi et trompe à eau
La trompe à eau, schématisée figure 2 est utilisée pour générer une dépression importante par effet Venturi à l’aide
d’un écoulement d’eau. Cela est mis à profit en chimie pour la filtration sur Büchner.
2015/2016 2/8

Lycée Newton - PT TMF - TD3 - Energétique des écoulements en conduite
Figure 2–Effet venturi et trompe à eau
On suppose l’écoulement parfait, homogène, incompressible, stationnaire dans le référentiel du laboratoire supposé
galiléen.
5.1. Préciser le sens physique de chacun des termes utilisés dans la phrase précédente.
5.2. A l’aide d’une équation de conservation de la matière, établir un lien entre la vitesse au point A(à la sortie
du robinet, dans le tube de rayon RA) et la vitesse en un point B(dans la zone de rétrécissement, de rayon
RB<RA).
5.3. A l’aide d’une équation d’évolution, en déduire la dépression PB−PAen fonction des rayons des tuyaux,
de la masse volumique µde l’eau.
5.4. La dépression est limitée par la pression de vapeur saturante de l’eau à la température ambiante qui est
Π(Tambiante ?
5.5. Calculer la vitesse maximale et le débit maximal du robinet dans ces conditions. Application numérique :
RA=1 cm et RB=0,2 cm.
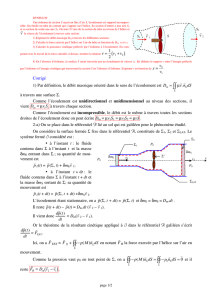
Ex 6 Etude d’une éolienne
On étudie l’interaction mécanique entre l’air en mouvement (le vent) et le rotor de l’éolienne. La description est faite
dans le référentiel terrestre RT, considéré comme galiléen. Il lui est lié une base cartésienne (ex,ey,ez). En amont, loin
de l’éolienne, le vent est uniforme et permanent, de vitesse v0=v0ex, et la pression est elle aussi uniforme, de valeur
notée P0. On suppose que les effets de la pesanteur sont négligeables à l’échelle de l’éolienne. On note ρla masse
volumique de l’air.
L’éolienne est formée très schématiquement d’un mât portant un rotor d’axe horizontal. La figure 3 montre un tube
de courant s’appuyant sur le pourtour du rotor de l’éolienne. La vitesse et la pression loin en amont sont uniformes
(v0et P0).
La pression loin en aval est uniforme et vaut P0. La vitesse loin en aval n’est uniforme que dans le tube de courant
et vaut vS.
2015/2016 3/8

Lycée Newton - PT TMF - TD3 - Energétique des écoulements en conduite
x
EB
A S
rotor
Figure 3 – Schéma du tube de courant freiné par l’éolienne.
IOn suppose que la perturbation apportée par le mât à l’écoulement de l’air est négligeable.
IOn ne s’intéresse pas aux détails de l’écoulement de l’air au voisinage du rotor et donc pas plus à la forme
précise des pales qui forment le rotor. Il suffira sonc de modéliser la surface balayée par ce dernier par un
disque de centre O, de diamètre Det d’axe (O,ex).
L’écoulement de l’air est supposé parfait (sauf au voisinage immédiat du rotor), stationnaire et incompressible. Il
présente une symétrie de révolution autour de l’axe (O,ex). On suppose que l’influence du sol est négligeable.
La section du tube de courant est supposée varier lentement avec x: on la note S(x). Elle varie d’une valeur SE, loin
en amont, à une valeur SS, loin en aval, en passant par une valeur SR=πD2
4au niveau du rotor.
Du fait de la variation lente de S(x), la vitesse peut être condidérée comme uniforme sur chaque section x=cte du
tube de courant, et dirigée selon ex(approximation), v=v(x)ex. En particulier, on considère qu’au niveau du rotor,
la vitesse du fluide est vR=vRex. On notera P(x) la pression dans le tube de courant à l’abscisse x. Dans le tube de
courant, on fait l’approximation de considérer l’écoulement comme uniforme loin en aval du rotor, vS=vSex. La
pression y est aussi uniforme, à la même pression qu’en amont.
On définit quatre sections E,A,B,Sdu tube de courant (voir figure 3). Les sections Aet Bsont situées de part de
d’autre du rotor, à sa proximité immédiate. On considérera ainsi que SA=SB=SRet que vA=vB=vR=vRex,
conformément au modèle de l’hélice plate. Enfin, la pression à l’extérieur du tube de courant est supposée non
modifiée par la présence de l’éolienne, et a donc la valeur uniforme P0. On node F=Fexla résultante des actions
exercées par l’éolienne sur l’air.
6.1. Etablir deux relations, l’une entre les grandeurs v0,vS,SEet SS, l’autre entre les grandeurs v0,vR,SEet SR.
Justifier l’évasement du tube de courant au niveau du rotor.
6.2. A l’aide d’un bilan de quantité de mouvement sur un système que l’on définira précisément, établir une
relation entre v0,vS,SE,ρet F.
6.3. A l’aide d’un bilan de quantité de mouvement sur un système que l’on définira précisément, établir une
relation entre PA,PB,SRet F. En déduire une relation entre v0,vS,ρ,Fet SR.
6.4. Déduire des questions précédentes l’expression de la vitesse vRde l’air au niveau du rotor, en fonction de
v0et vS.
6.5. Pourquoi l’écoulement ne peut-il pas être considéré comme parfait au voisinage immédiat du rotor ?
6.6. Déterminer l’expression de la puissance Pprélevée au vent par le rotor en fonction de ρ,SR,v0et du rapport
α=vS
v0.
6.7. Montrer que cette puissance Patteint une valeur maximale Pmax pour une valeur de αque l’on précisera.
Exprimer Pmax en fonction de ρ,SRet v0.
6.8. Définir le rendement énergétique ηde l’éolienne et donner son expression en fonction de α. Que vaut le
rendement maximal ηmax (formule de Betz des éoliennes) ?
6.9. On examine les fiches techniques de deux éoliennes de types très différents : une de faible puissance, destinée
à être montée sur un petit voilier pour l’alimenter en énergie électrique, l’autre de forte puissance, destinée à
produire de l’énergie électrique pour un réseau de distribution régional. Pour chacune, la fiche technique indique
(entre autres données) le diamètre Ddu rotor, la « vitesse nominale » v0du vent pour laquelle elle a été conçue
2015/2016 4/8

Lycée Newton - PT TMF - TD3 - Energétique des écoulements en conduite
préférentiellement, et pour laquelle elle fournit sa « puissance nominale » P. Les fiches techniques sont établies
en prenant pour masse volumique de l’air ρ=1,225 kg ·m−3. On rappelle qu’un nœud représente une vitesse de
1,852 km ·h−1.
faible puissance D=1,14 m v0=24 nœuds P=400 W
forte puissance D=47 m v0=15 m ·s−1P=600 kW
Commenter ces données à l’aide des résultats obtenus précédemment. On attend ici des commentaires faisant
appel à des arguments quantitatifs.
6.10. Déterminer la vitesse au bout d’une pale d’éolienne de forte puissance lors de son fonctionnement normal,
caractérisé par un demi-tour fait en une seconde. Pourrait-on envisager de construire une éolienne géante dont
le diamètre serait par exemple quatre fois supérieur ? Justifier la réponse.
6.11. L’étude d’une hélice de propulsion (avion, bateau, etc) est-elle différente de celle d’une éolienne ? Quels
sont les éléments qui diffèrent ?
Ex 7 Conduite forcée pour une canalisation hydroélectrique
Une conduite gravitaire amène l’eau (fluide parfait incompressible de masse volumique ρ) d’un barrage vers une
turbine de type Pelton. La conduite cylindrique, de diamètre constant D=30 cm, se termine horizontalement, son
axe étant situé à H=160 m au-dessous de la surface libre de l’eau dans le barrage de grande capacité. Le départ de
la conduite est H0=20 m au-dessous de la surface libre de l’eau, de niveau pratiquement constant (grande capacité).
Les frottements (et donc les pertes de charge) sont négligés.
injecteur
z
O
H
A la sortie de l’injecteur, à l’air libre, le jet d’eau frappe les augets de la turbine pour l’animer d’un mouvement de
rotation.
Pour les applications numériques, prendre : la pression atmosphérique P0=105Pa, l’accélération de la pesanteur
g=10 m ·s−2et ρ=103kg ·m−3.
Dans les questions 7.1 et 7.2, l’injecteur n’est pas encore en place.
7.1. Calculer la vitesse vAde l’eau à la sortie Ade la conduite (sans injecteur). A.N.
7.2. Que peut-on dire du champ des vitesses dans la conduite ? En déduire la loi de pression P(z) dans la
conduite. Montrer que l’on a un phénomène de cavitation (ébullition de l’eau sous très faible pression) dans une
région de la conduite à déterminer (on admet que la cavitation apparaît quand la pression devient voisine de
zéro). A.N.
On visse sur l’extrémité Aun injecteur (tubulure de section décroissante) de diamètre d<Det d’axe horizontal.
7.3. La vitesse d’éjection est-elle modifiée ? Et la vitesse dans la conduite ? Etablir la loi de variation P0(z) de la
pression dans la conduite et montrer que la cavitation y disparaît totalement (c’est le but recherché) pour d<d0;
calculer d0.
7.4. En prenant d=15 cm, calculer la vitesse vSde l’eau à la sortie Set le débit volumique QV. Calculer ensuite
la puissance cinétique du jet (son énergie cinétique par unité de temps), et montrer qu’elle s’exprime sous la
forme du produit de la pression cinétique (à évaluer) par le débit volumique.
Ex 8 Perte de charge singulière dans un élargissement
Un fluide incompressible de masse volumique ρs’écoule dans une canalisation cylindrique de section circulaire S1,
et d’axe horizontal Ox.
2015/2016 5/8