(chap 23 quadrilatères)

QUADRILATERES
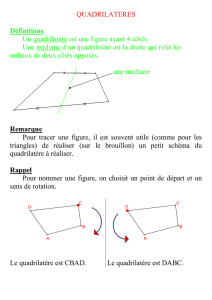
Pas de titre avant d'avoir fait l'intro
I Introduction :
Demander aux élèves des noms de figures
Carré triangle pentagone Hexagone.
Rectangle triangle rectangle
Losange triangle isocèle
Trapèze triangle équilatéral
Parallélogramme. Quadrilatère.
Ici nous allons étudier dans ce chapitre les quadrilatères.
II Vocabulaire :
1) Le quadrilatère :
Construire un quadrilatère quelconque
A B côté
D C sommet
diagonale
Les points A, B, C et D sont les 4 sommets de ce quadrilatère.
Les segments [AB], [BC] , [CD] et [DA] sont les 4 côtés de ce quadrilatère.
Les segments [AB] et [BC] sont 2 côtés consécutifs de ce quadrilatère.
Les segments [AB] et [DC] sont 2 côtés opposés de ce quadrilatère.
Les segments [AC] et [BD] sont les 2 diagonales de ce quadrilatère.
Les citer tous
Consécutif =1 lettre commune et opposés=pas de lettre commune
Pour nommer un quadrilatère on cite les sommets dans l'ordre où on les rencontre en parcourant les côtés.
Ce quadrilatère se nomme :
Elèves à l'oral
Préciser que l’on tourne dans le sens des aiguilles d’une montre en général
III Rectangle : Faire chercher la déf Quelles propriétés découlent de la figure ?
1) Définition :
Un rectangle est un quadrilatère …qui a 4 angles droits…………………………………….
Construis un rectangle ABCD tel que :
sa longueur soit L = AB = 4 cm et sa largeur soit = BC = 3 cm.
Construis les axes de symétrie de ce rectangle.
Son périmètre vaut en cm :
4 + 3 + 4 + 3 = 2 × 4 + 2 × 3 = 2 × ( 4 + 3 ) = 14 .
Le périmètre d'un rectangle de longueur L et de largeur est donné par :
L +
+ L + = 2 ×
××
× L + 2 ×
××
× = 2 ×
××
× Longueur + 2 ×
××
× largeur = 2 ×
××
× ( L + ) .
2) Propriété
Les axes de symétrie du rectangles sont les médiatrices de ses côtés.
ABCD BCDA CDAB DABC
ADCB DCBA CBAD BADC.

3) Propriété 2 :
Si un quadrilatère est un rectangle alors ses diagonales…se coupent en leur milieu et ont la même
longueur……………..……………………….……………………………………………………….
4) Propriété :
Construis un quadrilatère LOUP où :
• LU = OP = 5 cm
• [LU] et [OP] se coupent en leur milieu.
On voit que LOUP a ……4 angles droits……………………,
c'est donc un …rectangle………….…….
Propriété 3 : Si les diagonales d'un quadrilatère se coupent en leur milieu et ont la même longueur
alors ce quadrilatère est un rectangle.
Réciproque de P1
Dire que P1 et P2 différent( 1 part du rect et l'autre aboutit au rect)
5) Propriété 4 :
Si un quadrilatère est un rectangle …alors ses côtés opposés sont parallèles et de même longueur
…………………………………………….………………………………………………………………………..
A B
ABCD rectangle (AB) // (DC)
et
(AD) // (BC)
D C
Remarque : Est ce que tous les quadrilatères dont les côtés opposés sont parallèles et de même longueur sont
des rectangles ? …non il se peut qu’il n’y ait pas d’angle droit (par exemple le #)………………..
IV Le losange
1) Définition :
Un losange est un quadrilatère……qui a 4 côtés de même longueur.…….………………...
Construis un losange de côté 4 cm.
Construis les axes de symétrie de ce losange.
2) Propriété 1
Les axes de symétrie du losange sont ses diagonales
3) Propriété 2:
4) Propriété :
Construis un quadrilatère COUP tel que :
• (CU) ⊥ (OP)
• [CU] et [OP] ont le même milieu.
Si un quadrilatère est un losange alors ses
diagonales ……se coupent en leur milieu et sont
perpendiculaire
…………

On constate que COUP ……est un losange………………….
Propriété 3 : Si les diagonales d'un quadrilatère sont perpendiculaires et se coupent en leur milieu alors ce
quadrilatère est un losange.
5) Propriété 4 :
Si un quadrilatère est un losange alors ses côtés opposés sont parallèles deux à deux………..
6) Propriété 5 :
Si un quadrilatère est un losange alors ses angles opposés sont de la même mesure.
A
ABCD losange D B (AB) // (DC) et (AD) // (BC)
C
V Le carré
1) Définition :
Remarque : un carré est …un rectangle et un losange…………. .
Construis un carré ABCD tel que sa longueur soit a = AB = 5 cm. Son périmètre vaut en cm :
5 + 5 + 5 + 5 = 4 × 5 = 20 .
Le périmètre d'un carré de longueur a est donné par a + a + a + a = 4 ×
××
× a = 4 ×
××
× côté .
Construis les axes de symétrie de ce carré
2) Propriété 1 :
Les axes de symétrie d’un carré sont les médiatrices de ses côtés et ses diagonales
3) Propriété 2
Si un quadrilatère est un carré….…alors ses diagonales sont perpendiculaires, de même longueur et se
coupent en leur milieu……………………………………..
4) Propriété :
Construis TRUC tel que :
• (TU) ⊥ (RC)
• TU = RC = 4 cm
• [TU] et [RC] se coupent en leur milieu
On constate que les 4 côtés ……sont de même longueur…………………..……………
et que les 4 angles …sont droits………….alors c'est un …carré………….
Propriété 3 : Si les diagonales d'un quadrilatère sont perpendiculaires, de même longueur et se coupent en leur
milieu alors ce quadrilatère est un carré.
5) Propriété 4 :
Si un quadrilatère est un carré…alors ses côtés opposés sont parallèles deux à deux…………..
Un carré est un quadrilatère…qui a 4 angles droits et 4 côtés de
même longueur
………………………………………………………………….

VI Parallélogramme
Définition
Un parallélogramme est un quadrilatère …dont les côtés opposés sont parallèles………….
Construis un parallélogramme ABCD tel que :
AB = 5 cm et BC = 4 cm.
Compare à l'aide du compas les longueurs :
AB et CD puis AD et BC. Que remarques-tu ?
Les côtés opposés d'un parallélogramme ...
sont de même longueur.......
VII Le trapèze
Définition
Un trapèze est un quadrilatère ...ayant deux côtés opposés parallèles............................................................
Les côtés parallèles sont appelés ...les bases................................................
Construis un trapèze ABCD de …bases……
… [AB] et [CD] tel que AB = 7 cm et CD = 4 cm
VIII Le cerf-volant :
Envoyer des élèves au tableau tracer des cerf-volants tous différents jusqu’à obtention du chevron.
Que peux-tu dire des côtés de ce cerf-volant ?
1) Remarque :
Un cerf-volant a deux petits côtés consécutifs de même
longueur et deux grands côtés également de même longueur.
Que peux-tu dire des diagonales de ce cerf-volant ?
2) Propriété 1 :
Si un quadrilatère est un cerf-volant alors ses diagonales sont perpendiculaires.
3) Propriété 2 :
Une des diagonales du cerf-volant est un axe de symétrie de ce cerf-volant.
Que peut-on dire des angles opposés de ce cerf-volant ?
4) Propriété 3 :
Si un quadrilatère est un cerf-volant alors ses angles opposés sont de la même mesure.
Remarque :
1) Un trapèze qui possède un angle droit en possède en fait ..2.... , et s'appelle ......trapèze rectangle...........
2) Si un trapèze a ses deux côtés non parallèles de même longueur, c'est ......trapèze isocèle......................
Construis un cerf-volant MATH tel que :
MA = MH = 3 cm et AT = HT = 5 cm.
Tous les élèves de la classe ont-ils obtenu
le même cerf-volant ?…non..
B
L
O
C