PROBLEME 1 : MOTEUR ASYNCHRONE

97PYETRUN Page 1 sur 8
BACCALAUREAT TECHNOLOGIQUE
Session 1997
PHYSIQUE APPLIQUÉE
Série : Sciences et Technologies Industrielles
Spécialité: Génie Électrotechnique
Durée de l'épreuve : 4 heures Coefficient: 7
L'utilisation des calculatrices électroniques, programmables, alphanumériques ou à écran
graphique est autorisée, à condition que leur fonctionnement soit autonome et qu'il ne soit
fait usage d'aucune imprimante.
Chaque candidat ne peut utiliser qu'une seule machine sur sa table.
En cas de défaillance, elle pourra cependant être remplacée.
Cependant, les échanges de machines entre candidats, ainsi que les échanges d'information
par l'intermédiaire des fonctions de transmission des calculatrices sont interdits.
La justification complète et précise de chaque réponse, ainsi que le développement des
calculs intermédiaires, sont indispensables .Veiller également à la clarté de la présentation.
Tous ces éléments interviendront largement dans la note.
Veuillez numéroter toutes les questions traitées.
Le sujet ,constitué de 3 parties indépendantes, comporte 8 pages numérotées de 1 à 8 dont
le(s) document(s)-réponse(s) page(s) 6 , 7 et 8 sont à rendre avec la copie.

97PYETRUN Page 2 sur 8
PROBLEME I : MOTEUR ASYNCHRONE ( 9 points environ)
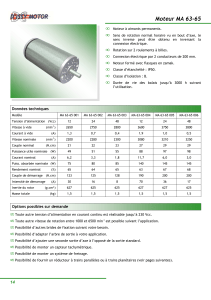
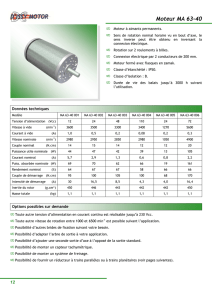
Sur la plaque signalétique d’un moteur asynchrone sont relevées les indications suivantes :
MOT. AS. TRI.
230 V / 400 V
50 Hz – 1440 tr.min-1
4,2 kW
1- Déduire de ces indications :
1.1) La vitesse de synchronisme ns de ce moteur alimenté sous 50 Hz.
Votre réponse devra être justifiée.
1.2) Le nombre de pôles du moteur.
2- Pour cette question, la fréquence de la tension d’alimentation est de 60 Hz. La vitesse
du moteur est alors égale à 1728 tr.min-1.
2.1) Déterminer la nouvelle vitesse de synchronisme.
2.2) En déduire la valeur du glissement.
3- On suppose que ce moteur possède, dans la plage de vitesse étudiée (partie linéaire de
la caractéristique), un couple de pertes mécaniques constant dont le moment, noté Tp,
vaut 2,0 N.m.
3.1) Quelle est l’origine de ces pertes ?
3.2) On note Tem le moment du couple électromagnétique du moteur.
Enoncer la relation existant entre Tem, Tu et Tp.
3.3) Représenter graphiquement sur le document-réponse annexe 1 la courbe Tu = f(n)
déduite de la courbe Tem = f(n) donnée sur le même document (courbe n°1 – f = 50 Hz).
3.4) Déterminer alors graphiquement la vitesse nv du moteur à vide.
3.5) A l’aide de cette même représentation graphique, déterminer le moment du couple
utile nominal de ce moteur.
3.6) En déduire la puissance utile nominale Pu du moteur.
4- A partir de sa représentation graphique annexe 1, déterminer l’équation du segment de
droite Tem = f(n) (courbe n°1).
5- Calculer alors dans les conditions nominales de fonctionnement du moteur, la valeur
de la puissance Ptr transmise au rotor.
6- On mesure la résistance R entre bornes du stator, à chaud. Pour cela, on utilise une
méthode voltampèremétrique, en courant continu. On détermine R = 2,0 Ω.
6.1) Faire un schéma du montage utilisé.
6.2) Pourquoi est-il nécessaire d’utiliser le courant continu dans cette méthode ?
6.3) Pourquoi cette méthode est-elle meilleure que la simple utilisation d’un ohmmètre ?
7 – Le moteur est alimenté par un réseau triphasé 230 V / 400 V, en charge nominale.
L’intensité du courant absorbée en ligne est I = 9,5 A.
7.1) Quel est le couplage utilisé ?
7.2) Calculer les pertes par effet Joule au stator.
7.3) Des essais à vide ont permis d’évaluer les pertes dans le fer au stator Pfs = 280 W.
Montrer que la puissance absorbée nominale vaut 5,26 kW. (on prendra Ptr = 4,71 kW).
7.4) Déterminer le rendement nominal du moteur.

97PYETRUN Page 3 sur 8
PROBLEME II :ASSERVISSEMENT DU MOTEUR (6 points environ)
On considère le même moteur que dans la partie I. Ce moteur est alimenté sous fréquence f
variable et sous une tension de valeur efficace U telle que le rapport U/f reste constant. Ceci
afin d’obtenir les caractéristiques mécaniques représentées par les courbes 1 à 4 de l’annexe 1.
1 – Quel type de dispositif permet de générer une tension alternative à fréquence variable, à
partir d’une tension continue ?
2 – On se propose de déterminer une équation générale de la famille de caractéristiques de
l’annexe 1. Par souci de simplification, dans tout ce problème, on négligera les pertes
mécaniques du moteur et on assimilera Tem à Tu. Ainsi, on ne parlera plus que du moment du
couple moteur qui sera noté T.
A chaque fréquence f correspond une vitesse de synchronisme ns (toujours exprimée en tr.min-1).
2.1) Montrer, par un calcul mené à partir de la représentation graphique des courbes 1 à 4, que
l’équation de ces courbes peut se mettre sous la forme générale : T = 0,5 (ns – n).
2.2) Déduire de la relation
60
.pn
fs
( p nombre de paires de pôles ; ns en tr.min-1) que, pour ce
moteur, la vitesse de synchronisme peut s’exprimer par la relation ns = 30f.
2.3) En déduire une expression de n en fonction de f et T.
3 – On souhaite traduire cette dernière équation n(f,T) par un diagramme symbolique utilisant
les opérateurs suivants, dont la signification est rappelée :
Compléter pour cela le schéma symbolique n°1 de l’annexe 2, en faisant figurer les
paramètres T, f, 2T, 30f et n, ainsi que les coefficients numériques 2 et 30.
4 – La vitesse n dépend donc des deux paramètres T et f.
4.1) Quelles seront les conséquences prévisibles sur la vitesse n de l’augmentation de T ?
4.2) Comment compenser une telle variation ?
5- Le moteur est placé dans le dispositif suivant, représenté schématiquement ci-dessous.
- On fixe sur l’axe du moteur un capteur de vitesse destiné à convertir celle-ci en une
tension proportionnelle à la vitesse n (tr.min-1) qui, exprimée en volts, s’écrit
ur = 6,67.10-3.n.
Ceci constitue la « chaîne de retour ».
- La tension ainsi produite est alors comparée à une tension de consigne continue uc.
- La tension u = uc – ur produite en sortie de l’opérateur de différence commande un
variateur de fréquence triphasé produisant une fréquence dont la valeur numérique
(en Hz) est égale à 10 fois celle de la tension u exprimée en volts.
k
s
e
s = k.e
-
+
e1
e2
ε
ε = e1 – e2
Opérateur de
différence
Variateur de
fréquence 3~
Moteur
asynchrone
Capteur de
vitesse
uc
u = uc -ur
f = 10.u
n(f,T)
ur = 6,67.10-3.n
+
-

97PYETRUN Page 4 sur 8
Lorsque tout ce dispositif fonctionne à vide (sans délivrer de couple mécanique), il peut être
modélisé par le schéma symbolique ci-dessous, regroupant les caractéristiques de chaque
élément :
5.1) Déterminer les valeurs des « transmittances » H et K pour que le schéma représenté ci-dessous
soit équivalent au précédent.
5.2) Quelle sera la valeur de ur si la vitesse du moteur est 1500 tr/min ?
5.3) Quelle devra être la valeur de u pour que le moteur tourne à cette vitesse ?
5.4) En déduire la valeur de uc dans ce cas.
5.5) On souhaite encore simplifier le schéma précédent de la manière suivante :
A étant la « transmittance globale » du montage.
Montrer alors que A peut s’exprimer en fonction de H et K de la manière suivante :
A =
H.K1 H
. Application numérique.
5.6) Retrouver la valeur de A à partir du résultat de la question d).
6- A partir du schéma symbolique complet du dispositif à vide, donné à la question 5 (page 4/8),
et de celui du moteur en charge demandé à la question 3 (annexe 2 – figure 1), compléter le
schéma symbolique n°2 de l’annexe 2, pour un fonctionnement en charge.
Faire figurer en particulier les paramètres uc, u, ur, n, f, T, 2T, 30f ainsi que les coefficients
numériques 10, 2, 30 et 6,67.10-3 .
7- Quel dispositif peut-on utiliser pour réaliser le capteur de vitesse de la chaîne de retour ?
10
30
6,67.10-3
uc
ur
n
n
n
f
u
comparateur
variateur de fréquence
moteur
+
-
capteur de vitesse
Schéma symbolique à vide
-
+
H
K
n
n
n
u
uc
ur
capteur de vitesse
A
n
uc

97PYETRUN Page 5 sur 8
PROBLEME III :REDRESSEMENT COMMANDÉ (5 points environ)
On considère le montage redresseur représenté sur l’annexe 3 –figure 1 : Pont de Graëtz
monophasé tout thyristors.
La charge est l’induit d’un moteur à courant continu à excitation constante, placé en série
avec une inductance L suffisante pour pouvoir supposer le courant constant dans cette charge
(lissage parfait).
On suppose également tous les thyristors utilisés parfaits.
La tension sinusoïdale u(t) d’alimentation du montage est délivrée par un transformateur. Elle
est représentée sur le document-réponse annexe 3 – figure 2 et a pour équation :
u(t) = 15.sin (100πt) , lorsqu’elle est exprimée en volts et t en secondes.
On déclenche les thyristors 1 et 3 à l’instant t = t0 (0 < t0 < T/2),
et les thyristors 2 et 4 à l’instant t0 + T/2.
1- Donner :
1.1) La valeur efficace U de u(t).
1.2) La valeur moyenne < u(t) > de u(t).
1.3) La fréquence f de u(t).
2- Compléter le tableau fourni en annexe 3 –figure 3.
3- D’un point de vue expérimental :
3.1) Comment visualiser un courant à l’oscilloscope ?
3.2) Modifier et compléter la figure 1 de l’annexe 3 afin de pouvoir visualiser simultanément
à l’oscilloscope le courant ic(t) dans la charge et la tension uc(t) aux bornes de la charge
(orientés sur cette figure). Indiquer le branchement de l’oscilloscope.
4- Si t0 = 2,5 ms, représenter graphiquement sur l’écran représenté annexe 3 – figure 4,
l’oscillogramme que l’on observerait pour uc(t), avec les réglages suivants :
Position DC – 2,5 ms/div. – 5 V/div.
Le niveau 0 V est placé au centre de l’écran.
5- Qu’observe-t-on si on passe en position AC ?
6- En utilisant les données numériques fournies précédemment, calculer la valeur moyenne de
la tension uc(t). On rappelle que dans ce cas :
< uc(t) > =
π
2.Ucmax
.cos (2.π.t0/T).
7- Expliquer quel est l’intérêt d’un pont à thyristors par rapport à un pont à diodes