TD Machine Synchrone Autopilotée 114.5 ko

MACHINE SYNCHRONE AUTOPILOTEE
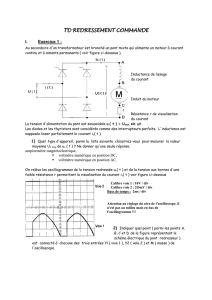
Un moteur synchrone est alimenté par l’intermédiaire d’un hacheur 4 quadrants et d’un pont à 6
thyristors.
Le hacheur délivre une tension que l’on assimile à sa valeur moyenne Ua.
Le pont à thyristors fonctionne en commutateur de courant ; grâce à une inductance suffisante L2, le
courant de circulation entre les deux convertisseurs est parfaitement lissé.
Afin d’assurer en permanence le synchronisme entre le rotor et le champ tournant créé par le stator,
ce qui évite tout risque de décrochage, les signaux d’amorçage des thyristors sont élaborés à partir
d’impulsions issues d’un capteur qui détecte la position du rotor. Ainsi il est possible de fixer le
déphasage  entre le fondamental du courant et la fém pour chaque enroulement du stator.
Ceci équivaut à fixer le retard angulaire  à l’amorçage des thyristors.
Le moteur ainsi contrôlé est dit autopiloté.
L2
K
L1
B
Io
v3
US
Hacheur
4Q
i3
Ua
Ca
uc
i2
i1
H
v2
v1
Enroulements
Statoriques
A
1 MODELISATION DE LA MACHINE.
Une machine synchrone triphasée dont les enroulements statoriques sont couplés en étoile possède 4
pôles. On a réalisé les essais suivants à la fréquence nominale de 50 Hz :
- ESSAI A VIDE : La caractéristique est une droite passant par l'origine. On donne un point :
- tension entre phases U = 220 V
- courant d'excitation Ie = 4,0 A
- ESSAI EN COURT-CIRCUIT : La caractéristique est une droite passant par l'origine. On donne un
point :
- courant en ligne : I = 3,5 A
- courant d'excitation : Ie = 1,0 A
- RESISTANCE entre phases R = 1,8 
On néglige les pertes mécaniques de cette machine ainsi que ses pertes dans le fer.
1-1 Donner le schéma équivalent d'une phase de la machine (tension simple et courant en ligne):
- on désignera par Xs la réactance synchrone et par r la résistance d'une phase.
- on flèchera la tension simple v, la fém e et l'intensité i du courant en ligne en convention
récepteur.
1-2 Calculer les éléments Xs et r du schéma équivalent. En déduire la valeur de l’inductance cyclique L
telle que Xs = L.
Page 1 / 6
N
Dans la suite du problème on supposera que la machine n'est jamais saturée, on négligera r et
on prendra Xs = 9,0 .
2 FONCTIONNEMENT EN COURANT SINUSOIDAL A FREQUENCE CONSTANTE:
La machine couplée à un réseau 127/220 V, 50 Hz fonctionne en moteur en absorbant une puissance
P = 1,0 kW avec un facteur de puissance de 0,87.
2-1 Calculer l'intensité en ligne et le moment du couple électromagnétique Te.
2-2 Tracer le diagramme vectoriel des tensions dans les deux cas possibles :  > 0 ou  < 0.
—
—
—
 est l'angle de déphasage de la tension v par rapport à l'intensité i du courant.
 est l'angle de déphasage de la f.é.m. e par rapport à i.
 est l'angle de déphasage de la tension v par rapport à la f.e.m. e appelé angle interne.
2-3 Déterminer pour chaque cas :
— La fém E.
— L'intensité Ie du courant d'excitation.
— La puissance réactive Q absorbée par le moteur.
— Préciser dans chaque cas si la machine est sous-excitée ou sur-excitée.
2-4 Montrer, en utilisant les diagrammes, que l'on a dans les deux cas :
V.cos  = E.cos 
2-5 Pour Ie = 5,0 A, on augmente progressivement, à partir d’une valeur nulle, la puissance que le
moteur fournit à sa charge.
2.5.1 Représenter sur un diagramme des tensions l’évolution du point représentatif du
fonctionnement.
2.5.2 Démontrer que la puissance du moteur peut s'exprimer sous la forme :
P 3
UE
sin  . Pour quelle valeur de  la puissance est elle maximale ?
Xs
2.5.3 Commenter le comportement de la machine au voisinage de cette limite.
3 TENSION ET FREQUENCE VARIENT SELON LA LOI :
V 127

 Cte
f
50
3-1 Rappeler la formule de Boucherot et en déduire que la f.e.m. s’écrit :
E  a Ie f.
A l'aide de l'essai à vide, calculer la valeur numérique de a .
Pour la suite de la partie 3, on maintient constantes les intensités Ie= 3A et I = 5 A.
3-3 Exprimer numériquement E, V et LI en fonction de f .
3-4 Représenter sur un même diagramme les tensions et forces électromotrices lorsque la fréquence
passe de 50Hz à 25 Hz (échelle 1cm  10V).
On fera figurer les angles ,  et . Que dire de ces angles quand f varie ?
3-5 Après avoir exprimé le moment du couple T e du moteur, montrer qu’il est indépendant de la
vitesse. Calculer sa valeur.
Page 2 / 6
4 ALIMENTATION PAR CONVERTISSEUR STATIQUE CONTINU/ALTERNATIF
On alimente la machine synchrone par un onduleur de courant triphasé à thyristors (figure 1, page 7).
Les thyristors sont supposés parfaits et l'on néglige la résistance de la bobine d'inductance L 1.
L'intensité Io et la tension Ua sont des grandeurs continues (constantes dans le temps).
Les tensions v1, v2, v3 sont sinusoïdales, leur valeur efficace commune est V. Elles forment un
système triphasé direct.
L'inductance L1 a un rôle de tampon entre les tensions Ua et uc (variable). Elle lisse le courant. Le
condensateur Ca a un rôle de tampon entre les courants d'intensités ia (variable) et Io . Il lisse la
tension.
4-1 On amorce les thyristors avec un angle de retard à l'amorçage  =
2
rad, soit 120° .
3
Représenter graphiquement les tensions vAN , vBN et uc en fonction de l'angle électrique  = t (sur le
document réponse n°1 ).
Remarque : sur le document réponse n° 1, on constate que le thyristor Th1 est amorçable pour  (en
radians) compris entre

7
et
.
6
6
.
4-2 Exprimer i1 en fonction de Io, lorsque :
- Th 4 conduit.
- Th 1 conduit.
- Th 4 et Th 1 sont bloqués.
En déduire la représentation graphique de i1 sur le document réponse n° 1.
4-3 Donner l'allure du fondamental if de i1; quel est le déphasage  entre if et v1 pour  =
2
rad?
3
En déduire que dans le cas général, les angles étant en radians :
=-
4-4 La tension moyenne redressée est donnée par :
ucmoy =
3 6
V cos 

En déduire l'expression de ucmoy en fonction de V et .
4-5 Déterminer l'expression de la puissance P absorbée par l'onduleur en fonction de V, Io et .
4-6 On rappelle d'autre part que les puissances absorbées par la machine sont données par :
P = 3 V If cos  et Q = 3 V If sin .
4-6-1 En déduire la valeur efficace If du fondamental de i1 en fonction de Io.
4-6-2 Montrer que Q est toujours négative. La machine doit-elle être sous-excitée ou sur-excitée
?
4-6-3 Application numérique :  = 120° ; Io = 3,0 A ; V = 127 v.
Calculer P, Q, If .
4-7 Montrer que : Ua = – ucmoy
En déduire l'expression de Ua en fonction de V et , puis en fonction de E et . (voir la question 2-4).
Page 3 / 6
5 AUTOPILOTAGE
Un capteur de position fixé sur le rotor commande les impulsions des thyristors. Dans ces conditions
l'angle  entre le fondamental du courant et la fém reste constant. De la même manière la fréquence
des courants est asservie à la vitesse angulaire  du rotor.
5-1 La fém E est proportionnelle à la vitesse de rotation et au courant d'excitation. On pose :
E = K Ie 
Calculer numériquement K lorsque E est exprimée en volts et  en radians par seconde (on rappelle
que la machine possède 4 pôles et qu'à vide E = 127 V pour Ie = 4,0 A).
5-2 Montrer en utilisant la relation du 4-7 que :
Ua = k 
Exprimer k en fonction de K, le et .
Avec les mêmes unités que précédemment, calculer numériquement k pour Ie = 4,0 A et  = - 30°.
1-4-3 Exprimer la puissance absorbée par l'ensemble "onduleur-moteur" en fonction de k, Io et .
Exprimer la puissance fournie par la machine en fonction du moment Te de son couple et de la vitesse
angulaire  ;
Exprimer Te en fonction de k et Io. On rappelle que les pertes dans l'onduleur sont négligeables.
Quelle relation lie Io et iamoy ?
1-4-4 La machine fonctionne en moteur et délivre un couple de 6,0 N m à la vitesse de 1 000 tr/min.
Calculer Ua et Io pour k = 1,6 v s/rad.
1-4-5 Cet ensemble est parfois appelé "machine à courant continu sans balais". Quels sont ses
avantages par rapport à la machine à courant continu classique ?
Page 4 / 6
L1
Io
B
K
ONDULEUR
v3
Th4
Ca
Ua
Th6
Th2
i3
v2
i2
v1
uc
i1
Th3
Th1
H
Enroulements
Statoriques
Th5
A
FIGURE 1
D1
T1
T2
D2
T3
D3
Uh
Us
ia
D4
L2
K

H

Ua
T4
FIGURE 2
Page 5 / 6
N
DOCUMENT REPONSE 1
I1
Io
0

2
-Io
Page 6 / 6