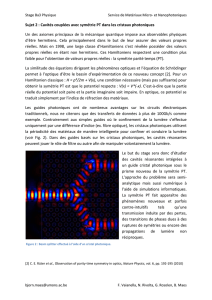
La Figure 4 montre le diagramme de bandes du cristal

1
Cristaux colloïdaux : bandes
photoniques interdites
BERTINO Rémi
MARI Arnaud L3 Physique 09/10
Encadrement : Jacques Persello

2
1. Introduction
Depuis près d’une dizaine d’années, l’intérêt des chercheurs vis-à-vis de l’étude et de la
synthèse des cristaux photoniques est croissant.
Les cristaux photoniques sont des structures périodiques de matériaux diélectriques et du
fait de cette périodicité, ces cristaux peuvent empêcher la propagation de la lumière dans
certaine gamme de longueurs d’ondes. Les ondes électromagnétiques sont alors diffractées
par le réseau, on peut donc parler de bandes interdites photoniques.
Les cristaux photoniques sont donc de formidables outils capables de stocker, filtrer ou
encore guider la lumière, susceptibles d’intéresser de nombreux domaines comme la
communication ou encore l’imagerie.
Notre travail s’est focalisé sur un certain type de cristaux photoniques, les cristaux
photoniques colloïdaux, c'est-à-dire des cristaux photoniques élaborés par l’assemblage de
particules colloïdales.
Les cristaux photoniques sont présents à l’état naturel sous plusieurs formes. L’exemple le
plus connu est l’opale, ce minéral semi précieux est composé de particules de silice de taille
comprise entre 200 et 400nm régulièrement disposées. Quand elle est exposée à la lumière
blanche, cette pierre a la particularité de présenter des reflets de plusieurs couleurs . Ce
phénomène optique est du à la diffraction. En effet, comme l’espace entre les particules est
de l’ordre de la longueur d’onde du visible, il va apparaître des interférences ce qui va
modifier l’onde lumineuse en sortie et ainsi crée cet aspect irisé.
(a) (b)
(a) Photo d’une opale (b) image MEB d’une opale de billes de silice de 287 nm de diamètre
D’autre exemples sont présents dans la nature, les papillons ou les souris de mer utilisent la
diffraction par un réseau de cristaux photoniques pour communiquer entre eux.
Ces structures sont des exemples naturels de matériaux appelés cristaux photoniques.
Dans cette synthèse, nous allons plus particulièrement nous intéresser à la notion de bande
interdite photonique (band gap en anglais).

3
2.Bandes interdites photoniques
2.1.Loi de Bragg
Un cristal photonique est une nano structure de matériau diélectrique où l’indice de
réfraction est périodiquement modulé. Il s’agit d’un cristal car le matériau est constitué par
un arrangement périodique de cubes élémentaires diélectriques d’indice de réfraction n1 et
n2.
Les cristaux photoniques existent sous une multitude de formes. Il existe néanmoins trois
principales catégories : unidimensionnel, bidimensionnel et tridimensionnel.
1D 2D 3D
Schéma des arrangements pour des cristaux photoniques unidimensionnels (1D), bidimensionnels (2D) et tridimensionnels
(3D). Les parties rouges représentent un indice de réfraction n1 et les parties jaunes n2.
Les cristaux photoniques affectent la propagation des ondes électromagnétiques de la
même manière qu'un potentiel périodique dans un cristal semi-conducteur modifie le
déplacement des électrons.
Ce modèle stipule qu'un électron dans un solide ne peut prendre des valeurs d'énergie
comprises dans certains intervalles que l'on nomme « bandes ». Il en existe deux types, les
bandes permises, et d'autres bandes dites interdites.
Dans un semi-conducteur, comme dans un isolant, les deux bandes autorisées sont séparées
par une bande interdite, appelée couramment « gap ». L'unique différence entre un semi-
conducteur et un isolant est la largeur de cette bande interdite, largeur qui donne à chacun
ses propriétés respectives.
Ce concept de bandes permises et interdites peut être étendu au comportement des
photons dans un cristal photonique. A cause de la variation périodique de l’indice de
réfraction, l’énergie des photons est quantifiée en bandes permises et en bandes interdites.
La loi de Bragg établit un lien entre la distance séparant les atomes d'un cristal et les angles
sous lesquels sont principalement diffractés des ondes électromagnétiques envoyés sur le
cristal.
On a la relation ci-dessous :
2d sinm 
 d = distance interréticulaire
 θ l’angle de Bragg(c’est le demi-angle de déviation)

4
 m = ordre de diffraction (nombre entier)
 λ = longueur d'onde
2.2.Explication géométrique de la Loi de Bragg
On considère donc un faisceau de photon envoyé sur un cristal avec un angle Ө. On s’attend
a ce que les ondes soit en partie transmises, et en partie diffractées.
Considérons tout d’abord deux rayons incidents parallèles diffusés par deux particules sur le
même plan (figure 1) :
(Figure 1)
On peux en tirer géométriquement la différence de marche entre les deux rayons :
d.cosd.cos
d(coscos)
Les interférences sont constructives uniquement si la différence de marche introduit un
déphasage multiple de 2π, c'est-à-dire si = mλ.
Cette condition implique que n 0 et 
On peux donc en conclure que les interférences constructives ont lieu dans une direction qui
correspond à la réflexion du signal incident sur le plan réticulaire.
On considère maintenant la réflexion de deux rayons incidents sur deux plans réticulaires
parallèles distants de d. (figure 2)
d

5
(Figure 2)
Notre construction implique que les angles BAD et DAC sont égaux et de valeur .
On peux donc aisément en tirer la différence de marche BD + DC = 2d sin 
Comme dans le cas précédent, nous avons des interférences constructives si m 
On retrouve donc bien la loi de Bragg : 2d sinm .
2.3.Conséquences de la Loi
Les bandes permises et interdites d’un cristal photonique se regroupent dans un diagramme
de bandes photoniques. C’est une représentation des fréquences possibles pour l’onde
électromagnétique au sein du cristal photonique en fonction de son vecteur d’onde, c'est-à-
dire sa direction de propagation au sein du cristal.
Pour expliquer ce phénomène de bandes interdites, nous prenons une représentation d’un
cristal à 3D frappé par des photons selon trois directions de propagation différentes.
Figure 3 : schéma d’un cristal photonique à 3D
et schéma de faisceaux de photon selon trois direction différentes
1
2
3