On étudie pour les belles de nuit un caractère qui est leur cou

LA COULEUR DES BELLES DE NUITS - Alizée
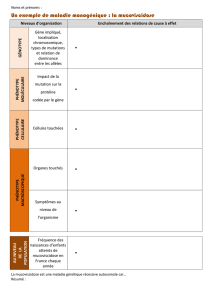
On étudie pour les belles de nuit un caractère : la couleur des fleurs. Ce caractère a trois états de caractères différents : la
couleur blanche, la couleur rose et la couleur rouge.
Hypothèse : Au caractère correspond un gène et à chaque état de caractère correspond un allèle.
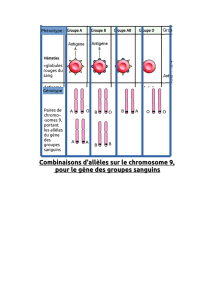
On aurait donc trois allèles : 'blanc', que l'on notera b, 'rose' que l'on notera r et 'rouge' que l'on notera R. Les phénotypes
correspondants sont notés entre crochets.
On croise deux parents P de lignées pures, donc homozygotes. Le parent de phénotype [R] est donc de génotype (R/R) et
produit 100% de gamètes (R). De même, le parent de phénotype [b] est de génotype (b/b) et produit 100% de gamètes (b).
On peut donc construire l’échiquier de croisement (F1) suivant :
On voit dans l’expérience que tous les individus (F1) sont de phénotype [r]. Pourtant,
l'allèle r n'est pas présent. Notre hypothèse de départ est donc fausse : il n'y a pas
d'allèle r qui détermine le phénotype [r].
D'où l'hypothèse :
Hypothèse : Au caractère correspond un gène avec deux allèles : R, qui détermine la couleur rouge, et b, qui détermine la
couleur blanche.
Examinons le résultat du premier croisement à la lumière de cette hypothèse. On voit dans l’expérience que tous les
individus (F1) sont de phénotype [r] et de génotype (R/b). On peut donc affirmer que, dans le cadre de notre hypothèse, les
allèles R et b sont codominants, c’est-à-dire qu’aucun allèle ne domine sur l’autre.
On croise ensuite deux individus issus de la descendance (F1). Ils sont tous les deux de phénotype [r] et de génotype (R/b).
Ils vont produire tous les deux 50% de gamètes (R) et 50% de gamètes (b). On peut donc construire l’échiquier de
croisement (F2) suivant :
On voit dans l’expérience que 25% des individus (F2) sont de
phénotype [R], 25% d'entre eux sont de phénotype [b] et 50%
d'entre eux sont de phénotype [r], ce qui est en accord à nos
résultats. Notre hypothèse semble donc juste. La rencontre des
gamètes est donc aléatoire, c’est-à-dire qu'un gamète possédant
l’allèle b a autant de chance de rencontrer un gamète possédant l’allèle b q'un allèle possédant l'allèle R.
Puis on croise deux parents de même phénotype issus de la descendance (F2). Les parents de génotype [R] sont de génotype
(R/R) et produisent 100% de gamètes (R). Les parents de phénotype [b] sont de génotype (b/b) et produisent 100% de
gamètes (b). Les parents de phénotype [r] sont de génotype (R/b) et produisent 50% de gamètes (b) et 50% de gamètes (R).
On peut dont construire les échiquier de croisement (F3) suivant :
On voit dans l’expérience que les individus issus de parents de phénotype [R] sont 100% de phénotype [R] ce qui est en
accord avec nos résultats. Notre hypothèse est alors juste ; il faut l’expression de deux allèles R pour que le phénotype [R]
apparaissent.
On voit dans l’expérience que les individus issus de parents de phénotype [b] sont 100% de phénotype [b] ce qui est en
accord avec nos résultats. Notre hypothèse est alors juste ; il faut l’expression de deux allèles b pour que le phénotype [b]
apparaissent.
On voit dans l’expérience que les individus (F3) issus de parents de phénotype [r] sont 25% de phénotype [R], 25% de
phénotype [b] et 50% de phénotype [r] ce qui est en accord avec nos résultats. Notre hypothèse est alors juste : la
ségrégation des exemplaires d’un gène lors de la formation des gamètes est aléatoire. C’est à dire que l’allèle b a autant de
chance de se retrouver avec l’allèle b ou l’allèle R.
100% (R)
100% (b) (R/b) 100%
100% (R)
100% (R) (R/R) [R] 100%
100% (b)
100% (b) (b/b) [b] 100%
50% (R) 50% (b)
50% (R) (R/R) [R] 25% (R/b) [r] 25%
50% (b) (b/R) [r] 25% (b/b) [b] 25%
50% (R) 50% (b)
50% (R) (R/R) [R] 25% (R/b) [r] 25%
50% (b) (b/R) [r] 25% (b/b) [b] 25%