Répétition 1 : Théorème de Thévenin et Norton 1

ELEN0075 – Électronique analogique – Répétition 1/1
Imprimé le 9 février 2006
Répétition 1 : Théorème de Thévenin et Norton
1 Rappels et définitions
1.1 Dipôle et théorème de superposition
Un dipôle électrique est un élément à deux bornes, caractérisé par le courant i qui le traverse
et par la tension v apparaissant à ses bornes :
Le dipôle électrique est dit linéaire si la relation i-v est une relation linéaire c'est à dire,
si 1 ii =pour une tension 1 v et
2
ii = pour une tension 2 v,
alors 21 biaii+= pour une tension 21 bvavv+= .
Exemples de composants linéaires :
• La résistance : R, R
v
i=
• L'inductance : L, dt
di
Lv=
• La capacité : C, dt
dv
Ci=
Un dipôle peut être lui-même composé d'un ensemble de dipôles interconnectés.

ELEN0075 – Électronique analogique – Répétition 1/2
Imprimé le 9 février 2006
Exemple :
Si la relation i-v est linéaire, on parle alors d'un circuit linéaire.
Remarques : dans le circuit précédent, on a introduit les sources suivantes :
La source de tension continue, vV
=
.
La source de courant continu,
i
I
=
.
Les circuits linéaires satisfont le théorème de superposition. La réponse du circuit à un
ensemble de sources indépendantes est donnée par la somme des réponses à chaque source
individuelle.
1.2 Application
Calculer la réponse du circuit (
v
) ci-dessous lorsqu'il n'est pas connecté à une résistance de
charge, c'est à dire lorsque 0
=
i en sortie du circuit.
Suggestion :
La réponse se calcule en 3 étapes successives. Toutes les sources étant indépendantes, on
calculera individuellement les contributions de chacune des trois sources. Lorsque l'on
s'intéressera à l'une des sources, les sources de courant seront remplacées par un circuit ouvert
et les sources de tension par un court-circuit. Ensuite on sommera toutes les contributions.
On trouve alors pour 0
=
i en sortie du circuit. : 21
21
121
21
2)( RR RR
IVV
RR R
v+ ++
+
=.

ELEN0075 – Électronique analogique – Répétition 1/3
Imprimé le 9 février 2006
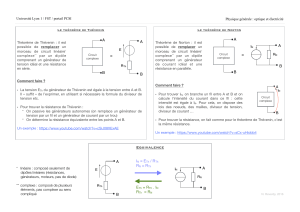
2 Théorème de Thévenin
On considère un circuit linéaire, composé d'éléments résistifs, de sources de tension
continues, et éventuellement de sources dépendantes linéaires, par exemples :
• Source de courant :
où 1 gvi=, avec 1 vqui est une tension apparaissant aux bornes d'un
autre élément du circuit.
Exemple d'une source commandée par une tension 1 v:
• Source de tension :
où 1 Avv=, avec 1 vqui est une tension apparaissant aux bornes d'un
autre élément du circuit.
Exemple d'une source commandée par une tension 1 v:
Ces sources commandées apparaissent dans des modèles de certains éléments d'électronique
(diodes, transistors,…) que l'on abordera ultérieurement.
Si l'on considère l'un de ces circuits. Sa caractéristique i-v étant linéaire, on a de façon
générale la relation suivante : BAvi
+
=
où A et B sont des constantes. On suppose 0
≠
Aet
0
<
A.
La droite i-v est appelée "droite de charge du circuit".
Prenons un exemple de circuit simple :
Le système nous donne : iRVvTHTH −= ,
et donc TH
TH
TH R
V
Rv
i+−= ou encore TH
R
A1 −= et TH
TH
R
V
B=

ELEN0075 – Électronique analogique – Répétition 1/4
Imprimé le 9 février 2006
Vu de l'extérieur, le circuit sous forme de boite noire ne peut être différencié du circuit
représenté dans sa forme complète, si l'on choisi TH
R
A1 −= et TH
TH
R
V
B=.
Le théorème de Thévenin établit que tout circuit linéaire peut-être remplacé par le circuit
simplifié qui reproduit sa droite de charge, c'est à dire :
Pour TH
R
A1 −= et TH
TH
R
V
B=,
≡
Ce théorème est très utile pour simplifier un circuit complexe en sous-circuits de Thévenin.
Calcul des paramètres du modèle équivalent de Thévenin :
Soit le circuit suivant :
Trois méthodes :
• Identification directe :
TH
V : tension apparaissant aux bornes du dipôle (de gauche) quand le circuit est ouvert
que l'on déduit par les lois de Kirchhoff.
TH
R : c'est la résistance équivalente du dipôle lorsque les sources de tension sont
mises à zéros.
• Par le calcul du courant CC I :
On détermine TH R comme dans la première méthode, mais au lieu de chercher VTH, on
calcule le courant CC Ii= qui traverse le dipôle si celui-ci est mis en court-circuit :
On a alors : TH
TH
CC R
V
I= soit : THCCTH RIV=.
• Méthode Vtest-Itest.
On impose un courant Itest et on calcule la tension aux bornes du dipôle, avec toutes les
sources continues mises à zéro. Cela nous permet de déterminer RTH.
On peut ensuite regarder le circuit ouvert pour déterminer VTH (Itest=0) ou déterminer
CC
I en court-circuitant le circuit (Vtest =0)
On trouve : V
RR R
VTH 21
2
+
= et 21
21 RR RR
RTH + =. Pour le calcul de TH R les sources de courant
continues seront remplacées par un circuit ouvert et les sources de tension continues par un
court-circuit. Les sources commandées seront discutées en détail ultérieurement.

ELEN0075 – Électronique analogique – Répétition 1/5
Imprimé le 9 février 2006
Remarques :
• Les trois méthodes sont équivalentes. Le choix de l'une par rapport à l'autre vient de la
pratique.
• Le théorème de Thévenin peut-être démontré (ici, nous n'avons fait que de montrer sa
validité avec quelques exemples). Il peut également être généralisé aux impédances
complexes ( LjZ
ω
=
ou Cj Zω
1
=).
3 Théorème de Norton
Comparons maintenant le circuit linéaire (le dipôle) au circuit équivalent suivant :
≡
Ce dernier à la droite de charge suivante, avec N
NI
R
v
i+−= et iRIRvNNN −= .
Le modèle équivalent de Norton n'est qu'une autre représentation du modèle équivalent de
Thévenin pour lequel on avait la droite de charge iRVvTHTH −= , TH
TH
TH R
V
Rv
i+−=
Le passage de l'une à l'autre des représentations se fait donc en identifiant IN à ICC et RNIN à
VTH et donc on trouve : TH
TH
NR
V
I= et THNRR =