Cinématique

Mécanique TP2 1
Cinématique
But : La manipulation consiste à étudier le mouvement d’un solide à partir d’un film vidéo, en
relevant image par image la position de son centre d’inertie. On peut ainsi remonter à l’évolution
temporelle des coordonnées de ce point, calculer sa vitesse et son accélération instantanées et
comparer ces résultats expérimentaux à la théorie.
(Pour des raisons de temps, vous travaillerez directement sur des fichiers vidéo sans avoir à filmer
vous-même les mouvements à étudier).
I - PRESENTATION DE LA TECHNIQUE.
Les mouvements étudiés ont été filmés avec un caméscope numérique grand public ayant des
vitesses d’obturation assez élevées (temps d’enregistrement d’une image de quelques ms) pour limiter
les effets de flou. Sur ce type d’appareil, la fréquence d’enregistrement des images est fixe : 25 images
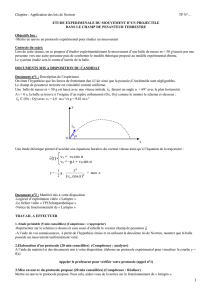
par seconde, soit 40 ms entre deux images. Comme le rappelle le schéma ci-dessous, l’objectif de la
caméra donne une image A’B’ d’un objet AB situé à une distance OA. La taille de l’image est
directement proportionnelle à celle de l’objet (définition du grandissement transversal, voir cours
d’optique). On pourra ainsi facilement remonter aux coordonnées cartésiennes d’un point objet B, en
déterminant les coordonnées de son point image conjugué B’ sur chaque image enregistrée.
O
A
B
A’
B’
plan objet
(plan du mouvement) plan image
(capteur CCD)
Objectif
caméra
y
y’
γ
= A’B’ / AB = y’/y = OA’ / OA
Grandissement transversal :
Coordonnée du point objet B :
y = y’ /
γ
Figure 1

Mécanique TP2 2
On voit également que par cette méthode, on se limitera à des mouvements à 2 dimensions dans un
plan perpendiculaire à l’axe optique de la caméra (pour rester à grandissement constant).
a- Détermination du grandissement transversal γ et des coordonnées d’un point objet :
Chaque image est composée d’un réseau de 704x576 pixels. La position d’un point image B’ sera
donnée par ses coordonnées (x’,y’) dans un repère cartésien plan muni d’une origine et de deux axes
perpendiculaires Ox (horizontal) et Oy (vertical). x’ et y’ seront exprimées en nombre de pixels. Les
coordonnées cartésiennes du point objet B conjugué de B’ seront données par :
x = x’/ γ et y = y’ / γ
x et y seront directement exprimés en mètres, à condition d’exprimer le grandissement γ en nombre
de pixels par mètre.
Ce grandissement sera déterminé à partir d’une distance étalon (de dimension connue) dans l’une des
deux directions Ox ou Oy (même grandissement, en raison de la symétrie de révolution de l’objectif
de la caméra). Soit ∆Y’
ét.
= (Y’
2
-Y’
1
) la dimension de cette distance étalon en nombre de pixels sur
l’image (dans la direction Oy par exemple) et ∆Y
ét.
sa dimension réelle en mètres. Le grandissement
transversal est donc donné par le rapport,
γ = ∆Y’
ét.
/∆Y
ét
(en nombre de pixels par mètre).
b- Précautions à prendre pour filmer le mouvement étudié :
- Le grandissement transversal dépend de la distance plan objet-objectif (voir figure 1).
L’objet étalon doit donc être placé dans le plan du mouvement.
- Pour la même raison, le plan du mouvement doit être perpendiculaire à l’axe optique de la
caméra (sinon le grandissement dépendra de la position de l’objet).
II- TRAITEMENT INFORMATIQUE DES FICHIERS VIDEO :
Le traitement informatique des fichiers vidéo se fera à l’aide du logiciel LatisPro qui permet de lire un
fichier vidéo image par image. A la première image, on définit un repère cartésien et la dimension de
la distance étalon. Puis on repère sur chaque image la position de l’objet étudié à l’aide de la souris.
Après avoir lu toutes les images de la séquence vidéo, le logiciel fournit un tableau à 3
colonnes donnant directement les coordonnées cartésiennes calculées (x,y) du point objet suivi et le
temps écoulé pour chaque point (à raison de 40 ms entre 2 points).

Mécanique TP2 3
A partir de ce tableau, on pourra calculer les coordonnées (v
x
, v
y
) du vecteur vitesse. Et on comparera
ces résultats expérimentaux à la théorie en simulant l’évolution temporelle de chacune de ces
coordonnées à l’aide de fonctions linéaires ou polynomiales que vous aurez préalablement
redémontrées.
III- ETUDE DE DIFFERENTS TYPES DE MOUVEMENT :
Nous allons étudier le mouvement d’une boule de pétanque dans le champ de pesanteur, en utilisant
deux conditions initiales différentes :
• sans vitesse initiale (chute libre _ mouvement rectiligne accéléré)
• avec vitesse initiale (mouvement parabolique).
III-1 Mouvement rectiligne accéléré dans le champ de pesanteur.
a- Traitement du fichier vidéo.
• Allumer votre PC et ouvrir le logiciel « LatisPro » par un double clic sur son icône visible
dans le bureau de Windows (pour l’utilisation de LatisPro, vous disposez d’une notice en
annexe à la fin de votre polycopié, et vous en trouverez également un exemplaire en salle de
TP, à laisser sur place).
• Faire l’acquisition image par image du fichier : cinématique 1.avi.
La distance étalon sera prise entre les deux marques noires sur la porte jaune en arrière plan
(elle mesure 1.90 m).
( suivre les instructions de la notice LatisPro « §1) lecture d’un fichier vidéo» )
Les coordonnées relevées, sont automatiquement sauvegardées dans les variables Mouvement
X et Mouvement Y auxquelles LatisPro affecte une abscisse « Temps » (40ms entre 2 images).
Ces variables sont disponibles dans la Liste des Courbes en cliquant sur le bouton
correspondant en haut à gauche dans la fenêtre principale. (notice §2)
• Editer les coordonnées dans le tableur :
Editer les variables « mouvement X », « mouvement Y » et « Temps » dans trois colonnes
distinctes du tableur (voir notice LatisPro § 3).
Vous pouvez vérifier que la variable Temps a bien été incrémentée de 40ms entre deux images
(prise de vues à 25 images/seconde) et que l’altitude Y de la balle diminue au cours du temps.
En revanche, vous pouvez également remarquer une légère dérive de la variable X (environ

Mécanique TP2 4
1cm sur un trajet Y de 2m). Cet artéfact est simplement introduit par un léger désalignement de
l’axe vertical de la camera par rapport à la verticale du lieu (environ 0.3°).
• Renommer les variables dans la liste des courbes et changer leur style d’affichage :
Dans la liste des courbes > double clic sur la variable « Mouvement Y » :
Dans le champ « nom de l’ordonnée », remplacer « Mouvement Y » par « Y ».
Cliquer sur « style » et choisir les croix non reliées (la ligne continue sera réservée aux courbes
de modélisation). Vous pouvez éventuellement changer la couleur des symboles.
Faire de même pour la variable « Mouvement X ».
• Visualiser la courbe y=f(t) sur la fenêtre n° 1 :
(voir la notice §4).
b- Détermination des coordonnées du vecteur vitesse.
Dans le repère (O,x,y) qui a été défini lors de l’acquisition, l e vecteur vitesse s’écrit :
x x y y
dOM
v v u v u
dt
= = + où M est un point fixe de l’objet suivi.
Le mouvement étant rectiligne le long de l’axe Oy, le vecteur vitesse a donc une seule composante :
v
x
= 0 et v
y
=
dt
dy où la composante vy à un instant t représente en fait la dérivée
de la fonction y = f(t) à cet instant t.
• Observer la courbe y = f(t) et décrire qualitativement l’évolution temporelle de la vitesse le long de
l’axe Oy, vy = f(t).
Donner le signe de v
y
et sa signification.
Préciser comment varie la valeur absolue de v
y
au cours du temps

Mécanique TP2 5
Calcul de v
y
:
On peut calculer v
y
en faisant l’approximation suivante : v
y
(t) =
dt
dy
≈
t
∆
y∆ =
1n1n
1n1n
tt yy
−+
−+
−
−
Où vy représente alors la vitesse moyenne (et non plus instantanée) du nième point sur l’intervalle de
temps ∆ t = tn+1-tn-1. Pour que cette approximation soit raisonnable il faut donc que ∆ t soit le plus petit
possible (dans notre cas ∆ t = 2x40 = 80 ms).
• Calculer vy dans la feuille de calcul de LatisPro (voir notice §5) calcul de dérivée).
• Vérification des calculs dans le tableur :
Cliquer sur l’onglet « tableur » en bas d’écran. Dans la liste des courbes, pointer la variable Vy et
la glisser dans une colonne du tableur.
Vérifier que la valeur de Vy calculée à la 4ième ligne par exemple est bien en accord avec la relation
suivante :
Vitesse au nième point : Vy(n) = [ Y(n+1) - Y(n-1) ] / [ Temps(n+1) – Temps(n-1) ].
• Ouvrir une nouvelle fenêtre graphique (fenêtre n°2) et visualiser la courbe vy = f(t).
(voir notice §4), on utilisera les symboles « + » non reliés entre eux pour tracer la courbe
(notice §4-e) changer de style).
L’évolution de vy en fonction du temps est-elle en accord avec l’analyse que vous en avez faite au
paragraphe précédent ?
(si ce n’est pas le cas, demander des explications à un enseignant).
Décrire plus précisément cette courbe : (type de fonction et vitesse initiale)
c- Détermination des coordonnées du vecteur accélération.
Le vecteur accélération est défini de la manière suivante : a =
dt
vd
=
dt
dv
y
y
u
L’accélération ay à un instant t le long de l’axe Oy représente donc la dérivée de la courbe vy = f(t) à
cet instant.
A partir de la courbe v
y
= f(t), décrire qualitativement l’évolution de l’accélération a
y
au cours du
temps.