Genératrice à courant continu Complet

EP3 La génératrice à courant continu (excitation shunt)
Page 1/4 Y.Sutra
I) Caractéristique en charge
1.1 Montage
On entraînera la génératrice à courant continu (ou dynamo) à l’aide d’un moteur asynchrone
triphasé.
1.2 Mesures
• On règle la tension à vide à sa valeur nominale.
• Ce réglage étnt fait, on ne touchera plus au rhéostat d’excitation
• On fera débiter la génératrice à courant continu dans le rhéostat de charge Rh, on relèvera
U et I, pour cela nous complèterons le tableau ci dessous.
• Recommencer les mesures en donnant une autres valeur à i (courant d’excitation).
Volmètre U (V) Ampèremètre I (A)
Calibre : C Division : D Lecture :L Valeur =
(C.L)/D Calibre : C Division : D Lecture :L Valeur = (C.L)/D
Rhéostat
de Charge
A
R=750 Ω
0,82 A
V
G
M3~
Rhéostat
d'excitation
i
I
U
Inducteur
Induit
3 x 400 V ~
A

EP3 La génératrice à courant continu (excitation shunt)
Page 2/4 Y.Sutra
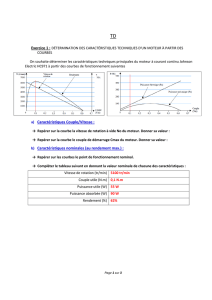
1.3 Graphes
Tracer les courbes U = f (I) pour différents courant d’excitation i sur le même graphique.
II) Courbe de réglage
C’est la courbe de l’intensité débitée en fonction de l’intensité d’excitation I = f (i) – U et n
restant constants.
2.1 Montage
Même montage que le précédent.
2.2 Mesures
• On règle la tension à vide à 180 V.
• La vitesse restant constante, on charge la dynamo à l’aide du rhéostat ce charge.
• On maintient la tension constante à l’aide du rhéostat d’excitation i.
• On relève le courant d’induit : I et le courant d’excitation : i.
Ampèremètre I (A) Ampèremètre i (A)
Calibre : C Division : D Lecture :L Valeur =
(C.L)/D Calibre : C Division : D Lecture :L Valeur = (C.L)/D
2.3 Graphes
Tracer sur un graphique I = f ( i )
i1 =
i2 =
U
I
Allure des courbes
N = ?
U = ?
i
I
Allure du graphe

EP3 La génératrice à courant continu (excitation shunt)
Page 3/4 Y.Sutra
III) Rendement de la dynamo shunt
Les pertes p comprennent :
♦ Les pertes par effet joule (Pj)
C’est la puissance dissipée en chaleur dans les enroulements de l’induit et dans l’inducteur,
calculable par la loi d’ohm.
♦ Les pertes mécaniques et pertes dans le fer, admises comme pertes constantes
Les pertes mécaniques se sont les pertes par frotfement (palier, balais, ventilation)
Les pertes dans le fer (pertes magnétiques) résultant de l’Hystérésis et des courants de
Foucault.
Détermination des pertes :
♦ Pertes par effet joule
 dans l’inducteur : p
d
= U . i
 dans l’Induit : p
i
= R
a
. Ia² = R
a
. ( I + i )²
♦ Pertes constantes : Pc
La somme Pc des pertes mécaniques et des pertes dans le fer est indépendante de la charge et
ne dépend que du flux dans l’induit et de la vitesse.
On fait tourner la génératrice en moteur à vide en excitation séparée tel que le flux inducteur φ
soit le même lorsque la machine fonctionne comme génératrice et avec la même vitesse n. La
puissance qu’il faut alors fournir au moteur est tout entière employée à compenser les pertes,
puisqu’elle produit aucun travail utile.
Or, puisque le flux inducteur et la vitesse sont les mêmes que lorsque la machine tourene en
génératrice, les perte spar hystérésis et courants de Foucault et les pertes mécaniques sont les
mêmes.
Elles s’obtiennent en retanchant de la puissance prise par le moteur les pertes par effet joules
dans cette machine, tournant à vide. C’est la méthode de « Swinburne ». (cela s’appelle faire le point à
vide de la dynamo)
La fém en génératrice est : E = N . n . φ
La fcém en moteur est : E’ = N . n . φ
Donc, nous aurons le même φ, si E = E’. Soit U la ddp aux bornes de la génératrice, on :
E = U + R
a
. I
Si on applique aux bornes de la machine, tourant en moteur à vide, une ddp U’ elle est traversée
par un courant I
0
et on a :
U’ = E’ + R
a
. I
0
η =
Pa
Pu
=
pPu
Pu
+
η
: Rendement
Pu : Puissance utile
Pa : Puissance absorbée
p : Puissance perdue, différentes pertes
G
Ia
iI
I
a
= I + i

EP3 La génératrice à courant continu (excitation shunt)
Page 4/4 Y.Sutra
3.1 Mesure de la résistance d’induit : Ra
Plusieurs montage peuvent être utilisé :
 Le montage volt-ampèremétrique.
 Lecture directe grâce a un ohmmètre.
On effectuera cette mesure juste aussitôt l’essai en charge pour connaître la résistance à chaud.
3.2 Calcul de rendement de la machine au point nominal
A
V
U1
220 V
I
G
Induit
U
+
−
ΩG
Induit
Méthode volt - ampèremétrique Mesure directe à l’ohmètre