au format WORD

Session de 1978 – Deuxième épreuve – 3 heures
PREMIER PROBLEME - (20 points)
Une génératrice à courant continu porte sur sa plaque signalétique : puissance utile 3 kW ;
tension d'induit 220 V ; courant d'induit 13,6 A ; vitesse 1 500 tr/min.
On donne pour cette machine :
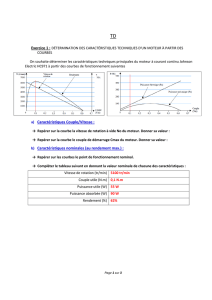
 la caractéristique à vide donnant la f.e.m. à vide E0 en fonction du courant d'excitation Id, à vitesse
nominale ; cette caractéristique est tracée sur le graphe joint ;
 la chute de tension  due à la réaction magnétique d'induit en fonction du courant induit Ia :
Ia (ampères)
0
2
4
6
8
10
12
13,6
15
 (volts)
0
0,4
0,8
1,6
2,5
3,6
5,1
6,5
7,9
Ces valeurs de  sont données pour la vitesse nominale et on rappelle que  est
proportionnelle à la vitesse.
 les résistances mesurées à chaud : Ra = 1,7  pour l'induit et Rd = 180  pour l'inducteur.
1. La génératrice est utilisée en excitation dérivation.
On néglige le courant inducteur devant le courant induit.
1.1. Calculer la résistance critique du rhéostat d'excitation qui permet l'amorçage de la
génératrice à la vitesse nominale.
1.2. Calculer la résistance du rhéostat d'excitation pour que la génératrice fonctionne à son
point nominal.
1.3. La génératrice, entraînée à la vitesse n = 1200 tr/mn, débite son courant nominal. Calculer
la tension d'induit sachant que le rhéostat d'excitation a une résistance Rhd = 106 .
2. Afin de déterminer le rendement de la génératrice fonctionnant à son point nominal, on effectue
un essai en moteur à vide, excitation séparée. On relève :
tension d'induit U0 = 245 V ; courant d'induit I0 = 1 A ; vitesse n = 1 500 tr/min.
2.1. Justifier le choix de la tension d'induit U0.
2.2. Calculer le courant d'excitation de la machine dans cet essai.
2.3. Calculer le rendement de la génératrice au point nominal.
3. La génératrice est utilisée en excitation séparée pour charger 15 batteries d'accumulateurs
identiques, branchées en série. Chaque batterie a une f.e.m. de 12 V et une résistance interne de 0,1 .
On veut, en agissant sur le courant d'excitation Id, maintenir un courant de charge constant et égal à
10 A lorsque la vitesse d'entraînement de la génératrice varie de 1300 tr/min à 1700 tr/min.
Calculer le courant d'excitation Id à utiliser pour les cinq valeurs de la vitesse :
1300, 1400, 1500, 1600, 1700 tr/min.

E0(V)
200
150
100
50
0Id
0,5 1,0 1,5
Caractéristique à vide
E0 = f(Id) à nn = 1500 tr/mn
échelles : 1 cm pour 0,1 A
1 cm pour 10 V

DEUXIEME PROBLEME - (20 points)
On se propose d'étudier deux montages redresseurs utilisant des thyristors. On supposera ces
thyristors parfaits c'est-à-dire qu'ils ont une tension entre anode et cathode nulle quand ils sont passants
et que leur courant de maintien est nul (blocage quand i passe par zéro).
Ces montages sont alimentés par un système de tensions triphasées équilibrées sinusoïdales de
valeur efficace entre phase et neutre V = 220 V, de fréquence 50 Hz s'écrivant :
ωtsin2Vv1
;
 3
2
ωtsin2Vv2
;
 3
4
ωtsin2Vv3
.
Les thyristors sont supposés commandés les uns après les autres par des impulsions séparées
par un tiers de période T du système de tensions, soit :
le thyristor 1 commandé à t0 , le thyristor 2 à t0 + T/3, le thyristor 3 à t0 + 2T/3 ….
On introduira l'angle de retard  à l'amorçage par rapport à la conduction naturelle par diodes en
remarquant que
6
ωt
12
T
tω00 
.
Les graphes seront effectués avec les échelles suivantes et seront tracés sur la feuille-réponse
comportant les courbes jointes au texte :
cm 4 V2220 
cm 1 A1 
cm 12s 0,02T 
Partie A : Le dipôle « charge » est purement résistant de valeur R = 200 
La première impulsion arrive sur le thyristor Th1 à t0 = T/4 soit  = /3.
1. Représenter graphiquement en fonction du temps la tension uc aux
bornes de la charge en régime établi.
2. Calculer la valeur moyenne Ucmoy de la tension uc(t) puis la valeur
moyenne Pc de la puissance consommée dans la charge.
3. Déduire de l'expression de Pc la valeur efficace commune I de i1 , i2 et i3
et calculer le facteur de puissance
IV3P
fc
p
du montage.
Parti B : Le dipôle « charge » impose ic constant et égal à 2 A.
La conduction est alors ininterrompue, un thyristor se bloquant quand
l'autre s'amorce. Le retard à l'amorçage est  avec 0 ≤  ≤ 2/3.
1. Représenter pour  = /3 la différence de potentiel uc et le courant i1
dans la phase 1, en fonction du temps.
2. Calculer la valeur moyenne Uc’moy de uc(t) et montrer qu'elle s'écrit :
cos
2π
6V3
'U moyc
.
3. Calculer la valeur efficace commune I’ de i1, i2 et i3.
4. Calculer la puissance moyenne Pc' mise en jeu dans la charge et conclure en étudiant le signe de
cette puissance en fonction de  , sur le fonctionnement générateur ou récepteur du dipôle « charge ».
5. Calculer le facteur de puissance
I'V3 'P
'f c
p
et donner sa valeur maximale.
i1
i3
i2
Th1
Th2
Th3
ic
1
1
3
2
nuc
CHARGE
i1
i3
i2
Th1
Th2
Th3
ic
1
1
3
2
nuc
CHARGE

tensions
0t
tensions
0t
QUESTION A1
QUESTION B1
T
T
T/12 t0
i1
0t
T