2007-08.cours.chapitre-5.convexite.mdr2017-04-27

EFREI 2007-2008
Chapitre 05 :
Convexité.

1 Convexité des fonctions d’une variable réelle
Soit Iun intervalle de R.
1.1 Définition et interprétation géométrique
Définition 1.1 — Soit f:I→R.
1. On dit que fest convexe lorsque :
∀(x1,x
2)∈I2,∀α∈[0,1],f(αx1+(1−α)x2)≤αf (x1)+(1−α)f(x2).
2. Lorsque −fest convexe, on dit que fest concave.
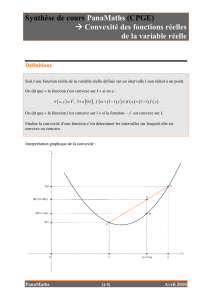
– Remarque – Ceci signifie que tous les points de l’arc « M1M2» sont situés sous la corde [M1M2]:
Exemple 1.1 – Les fonctions affines, la fonction carré x7→ x2, la fonction x7→ |x|.
1.2 Inégalités de convexité
Proposition 1.1 — (Inégalité de Jensen) Soit n≥2et f:I→Rune fonction convexe. Alors :
∀(λ1,...,λ
n)∈Rn
+,
n
X
i=1
λi=1,∀(x1,...,x
n)∈In,f
n
X
i=1
λixi!≤
n
X
i=1
λif(xi).
Démonstration — Récurrence sur n.
1. Pour n=2, c’est la définition de la convexité.
2. Supposons le résultat vrai au rang net vérifions-le au rang n+1. Soit donc (λ1,...,λ
n+1)∈Rn+1
+tels que
Pn+1
i=1 λi=1et (x1,...,x
n+1)∈In+1 .
Si λn+1 =1, alors tous les autres λisont nuls donc l’inégalité est une trivialité, c’est même une égalité.
Sinon, remarquons que
f n+1
X
i=1
λixi!=f n
X
i=1
λixi+λn+1xn+1 !.
Posons y=Pn
i=1 µixiet pour tout iµ
i=λi
1−λn+1
. Ainsi pour tout iµ
i≥0et Pn
i=1 µi=1;yest alors un barycentre
à coefficients positifs des xidonc y∈I.Ona
f n+1
X
i=1
λixi!=f((1 −λn+1)y+λn+1 xn+1)
d’où, par convexité de f:
f n+1
X
i=1
λixi!≤(1 −λn+1)f(y)+λn+1 f(xn+1 ),

c’est-à-dire
f n+1
X
i=1
λixi!≤(1 −λn+1)f n
X
i=1
µixi!+λn+1f(xn+1 ).
D’après l’hypothèse de récurrence :
f n+1
X
i=1
λixi!≤(1 −λn+1)
n
X
i=1
µif(xi)+λn+1f(xn+1)=
n+1
X
i=1
λif(xi),
ce qui achève la récurrence. 
1.3 Caractérisation géométrique
Soit f:I→R.
Proposition 1.2 — fest convexe si et seulement si son épigraphe E={(x, y)∈I×R;y≥f(x)}est un ensemble
convexe du plan : ∀(M, N)∈E,[M, N]⊂E.
Démonstration —
=⇒Supposons fconvexe et soit Eson épigraphe. Soit M(x1,y
1)∈E,N(x2,y 2)∈E et A(x, y)∈[M, N]. Alors il
existe α∈[0,1] tel que x=αx1+(1−α)x2et y=αy1+(1−α)y2. Par convexité de f:
f(x)=f(αx1+(1−α)x2)≤αf(x1)+(1−α)f(x2).
Or (M, N)∈E
2donc αf(x1)+(1−α)f(x2)≤αy1+(1−α)y2. D’où f(x)≤y, c’est-à-dire A∈E.
⇐=Supposons que Eest convexe. Soit (x1,x
2)∈I2et M,Nles deux points du graphe de fd’abscisses respectives
x1et x2. D’après l’hypothèse, [MN]∈E.
Soit alors α∈[0,1] et x=αx1+(1−α)x2. Posons y=αf(x1)+(1−α)f(x2).OnaB(x, y)∈[MN], donc B∈E,
d’où f(x)≤y, et ainsi f(αx1+(1−α)x2)≤αf (x1)+(1−α)f(x2): c’est la définition de la convexité. 
Proposition 1.3 — fest convexe (respectivement concave) sur Isi et seulement si :
∀(x, y, z)∈I3, x<y<z =⇒f(x)−f(y)
x−y≤f(x)−f(z) x−z≤f(y)−f(z) y−z(respectivement ≥).
Démonstration —
=⇒Soit (x, y, z)∈I3tel que x<y<z. Il existe α∈[0,1] tel que y=αx +(1−α)z. Donc y−x=(α−1)(x−z)
et y−z=α(x−z).Orfest convexe d’où f(y)≤αf (x)+(1−α)f(z). Ainsi
f(x)−f(y)
x−y≤(α−1)(f(x)−f(z)) (α−1)(x−z)et f(z)−f(y) z−y≤−α(f(x)−f(z)) −α(z−y),
d’où la double inégalité recherchée.
⇐=Supposons que pour tous (x, y, z)∈I3,f(x)−f(y)
x−y<f(y)−f(z) y−z(on n’a pas besoin de plus). Soit (x1,x
2)∈
I2,α∈]0,1[ et x=αx1+(1−α)x2∈I. Alors x1<x<x
2donc
f(x1)−f(x)
x1−x≤f(x)−f(x2) x−x2
.
Or x1−x=(1−α)(x1−x2)et x−x2=α(x1−x2), d’où
f(x1)−f(x)
(1 −α)(x1−x2)≤f(x)−f(x2) α(x1−x2),
soit
α(f(x1)−f(x)) ≥(1 −α)(f(x)−f(x2)),
et ainsi f(x)≤αf (x1)+(1−α)f(x2). Par conséquent fest bien convexe. 
Exemple 1.2 – fest convexe et concave sur Isi et seulement si la fonction (x, y)7→ f(x)−f(y)
x−yest constante sur
I×I, c’est-à-dire si et seulement si fest une fonction affine.

1.4 Caractérisation des fonctions convexes dérivables
Proposition 1.4 — Soit f:I→Rdérivable. fest convexe (resp. concave) sur Isi et seulement si f0est croissante
(resp. décroissante).
Démonstration —
=⇒Supposons fconvexe et soit (x1,x
2)∈I2tel que x1≤x2. Alors pour tous (x0
1,x
0
2)∈i2tel que x0 1≤x1et
x2≤x0
2,ona
f(x1)−f(x0
1)
x1−x0
1
≤f(x2)−f(x0
2)
x2−x0
2
par transitivité de la relation ≤. On passe alors à la limite successivement lorsque x0
1tend vers x1puis x0 2vers x2,
obtenant ainsi que f0(x1)≤f0(x2). Par conséquent f0est croissante et fest convexe.
⇐=Soit (x, y, z)∈I3tel que x<y<z. D’après le théorème des accroissements finis, il existe c1∈]x, y[et c2∈]y, z[
tels que f(x)−f(y)
x−y=f0(c1)et f(y)−f(z) y−z=f0(c2). Grâce à la croissance de f0,f(x)−f(y) x−y≤f(y)−f(z) y−z, ce qui
nous donne la convexité de fd’après la démonstration de la proposition 3.2. 
Exemple 1.3 – ln est concave sur R∗
+et exp est convexe sur R.
Corollaire 1.1 — Soit f:I→Rdeux fois dérivable.
1. fest convexe sur Isi et seulement si f00 ≥0sur I.
2. fest concave sur Isi et seulement si f00 ≤0sur I.
1.5 Position de la courbe par rapport à la tangente
Proposition 1.5 — Soit f:I→Rdérivable. fest convexe sur Isi et seulement si son graphe est situé au-dessus
de chacune de ses tangentes, c’est-à-dire :
∀(x, a)∈I2,f(x)≥f(a)+(x−a)f0(a).
Démonstration —
=⇒D’après le théorème des accroissements finis, il existe ccompris entre aet xtel que f(x)=f(a)+(x−a)f0(c).
D’après la convexité de f, la dérivée f0est croissante donc :
•si a≤c≤xalors f0(c)≥f0(a);orx−a≥0, d’où f(x)≥f(a)+(x−a)f0(a);
•si x≤c≤aalors f0(c)≤f0(a);orx−a≤0, d’où f(x)≥f(a)+(x−a)f0(a).
⇐=Pour tous (a, b)∈I2,onaf(b)≥f(a)+(b−a)f0(a)et f(a)≥f(b)+(a−b)f0(b). En sommant ces deux
inégalités on obtient 0≥(b−a)(f0(a)−f0(b)), donc f0est croissante, d’où fest convexe. 
Exemple 1.4 – ∀x∈R,e
x≥1+xet ∀x>−1,ln(1 + x)≤x.
2 Convexité des fonctions de plusieurs variables réelles
2.1 Définition
Définition 2.1 — Une partie Ωde Rnest convexe si ∀(M, N)∈Ω2,[MN]⊂Ω.
Exemple 2.1 – Sont convexes dans Rn: les boules, les sous-espaces vectoriels.
Dans toute la suite de la section, Ωdésignera une partie ouverte et convexe de Rn.

Définition 2.2 — Soit f:Ω→R.
1. On dit que fest convexe lorsque :
∀(x, y)∈Ω2,∀t∈[0,1],f(αx +(1−α)y)≤αf(x)+(1−α)f(y).
2. Lorsque −fest convexe, on dit que fest concave.
Exemple 2.2 – 1. Les formes linéaires f:Rn→R,x7→ Pn
i=1 aixi, sont convexes.
2. Soit p>2et f:Rn→Rdéfinie pour tout x=(x1,...,x
n)∈Rnpar f(x)=Pn
i=1 |xi|p. Alors fest convexe.
Proposition 2.1 — Soit f:Ω→R.fest convexe sur Ωsi et seulement si pour tous (x, y)∈Ω2la fonction
fx,y :[0,1] →Rdéfinie par fx,y(t)=f((1 −t)x+ty)est convexe.
Démonstration —
=⇒Soit (x, y)∈Ω2,(s, t)∈[0,1]2et α∈[0,1]. Alors :
fx,y(1 −α)t+αs=fx+ ((1 −α)t+αs)(y−x)=f(1 −α)(x+t(y−x)) + α(x+s(y−x))
≤(1 −α)f(x+t(y−x)) + αf (x+s(y−x)) = (1 −α)fx,y(t)+αfx,y(s),
donc fx,y est bien convexe.
⇐=Soit (x, y)∈ωet t∈[0,1]. Alors :
f((1 −t)x+ty)=fx,y(t)=fx,y((1 −t)×0+t×1) ≤(1 −t)fx,y(0) + tfx,y(1) = (1 −t)f(x)+tf(y),
donc fest bien convexe. 
2.2 Caractérisation des fonctions convexes différentiables
Définition 2.3 — Soit f:Ω→Rune fonction de classe C2sur Ω. La hessienne de fen a∈Ωest la matrice
Hf(a)=∂2f
∂xi∂xj
(a)1≤i,j≤n ∈Mn(R). D’après le théorème de Schwarz, cette matrice est symétrique.
Proposition 2.2 — Soit f:Ω→Rune fonction de classe C2sur Ω. Alors fest convexe sur Ωsi et seulement si
pour tout a∈Ωla hessienne Hf(a)est une matrice positive (au sens de la définition 3.2).
Démonstration — Pour tout (x, y)∈Ω2, l’application fx,y est de classe C2sur [0,1] et on a pour tout t∈[0,1] :
f0
x,y(t)=
n
X
j=1
∂f
∂xj
((1 −t)x+ty)(yj−xj)
=−−→ grad(f)((1 −t)x+ty)·(y−x),
f00
x,y(t)=
n
X
i=1 
n
X
j=1
∂2f
∂xi∂xj
((1 −t)x+ty)(yj−xj)
(yi−xi)
f00
x,y(t)=t(y−x)Hf((1 −t)x+ty)(y−x).
=⇒Supposons d’abord que fest convexe sur Ω. Soit a∈Ωet u∈Rn.Siε>0est tel que a+εu ∈Ω, alors
d’après la proposition 2.1 l’application fa,a+εu est convexe. Par conséquent d’après le corollaire 2.1 :
0≤f00
a,a+εu(0) = t(a+εu −a)Hf(a)(a+εu −a)=ε2tuH
f(a)u
et ainsi la matrice Hf(a)est positive pour tout a∈Ω.
⇐=Supposons que pour tout a∈Ω,Hf(a)est positive. Soit (x, y)∈Ωet t∈[0,1]. Alors
f00
x,y(t)=t(y−x)Hf((1 −t)x+ty)(y−x)≥0