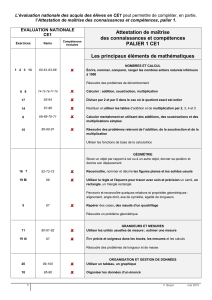
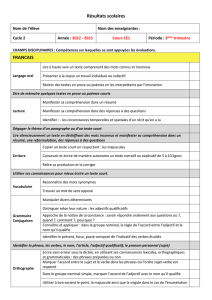
1. Introduction - Cours en Ligne

d
d
x y
z E
x y z E z x y
x y z

x y x y y x
+
A B
β B x
β y
A x y y x
B
x x
f
f E x x+f=f+x=x
f0~ 0 0
f f f0
f=f+f0=f0
f
x f
x
x
x x0E
x+x0=f
x0x−x
x y z (x+y) + z=x+ (y+z)

(x−y)−z x −(y−z) =
x−y+z
E+ (E, +)
λ x E λx E
E
λ E
λ µ x E λx +µx = (λ+µ)x
λ
λ
λ x y E λx +λy =λ(x+y)
λ

λ µ x E λ(µx) = (λµ)x
x2x=f0.5(2x) = f(0.5∗
2)x=x
1
x E 1x=x1
λ
2λ
E
x y x +y∈E
x y x +y=y+x
0∈E x x+0 = 0+x=x
x x0E x +x0= 0
x y z (x+y) + z=x+ (y+z)
λ x E λx ∈E
λ µ x E λx+µx = (λ+µ)x
λ x y E λx +λy =λ(x+y)
λ µ x E λ(µx)=(λµ)x
x E 1x=x
E+
E x E
F E
E E
E
λ1, λ2, ...λkk x1x2xk
E x1x2xk
λ1λ2λk
x=λ1x1+λ2x2+... +λkxk

x E
F E
F
E
f= 0 x−x= (−1) x
E F
2 2 ={(a, b), a ∈
, b ∈ } 2
(a, b)+(c, d)=(a+c, b +d)
λ(a, b)=(λa, λb)2
2(a, b)+(c, d)=(a+c, a +d, b +
c, b +d)λ(a, b)=(λa, λb)
2
2(a, b)+(c, d)=(a+d, b +c)
λ(a, b) = (λa, λb)2
2
λ(a, b)=(λa, 0) 2
2
λ(x, y) = (λ2x, λ2y)2
E
E
2 2 =
{(a, b), a ∈, b ∈ } 2
(a, b)+(c, d) = (a+c, b +d)
λ(a, b) = (λa, λb)2
F f(x) = aexp(x)+
bexp(−x)a b F f +g
x f(x) + g(x)