Bras de robot à muscles artificiels Extrait du sujet Concours

MPSI/PCSI TD n°5 SLCI Pôle Kerichen-Vauban
Page 1/7
Bras de robot à muscles artificiels
Extrait du sujet Concours Commun Polytechnique 2001
Présentation :
L’utilisation de l’énergie pneumatique pour l’actionnement des manipulateurs présente des propriétés qui peuvent
s’avérer intéressantes pour les applications en milieu hostile ou de type biomécanique :
 l’absence de forts courants électriques écarte les risques d’explosion et réduit à néant les interférences
électromagnétiques.
 les muscles artificiels sont économiques. Ils engendrent des forces de contraction du même type que celles
produites par les muscles humains. Leur puissance massique est très élevée par rapport à un actionneur classique.
Enfin, ils présentent naturellement une faible rigidité qui peut être mise à profit pour limiter les conséquences des
collisions et faciliter les tâches d’assemblage.
 En matière de préhension, l’usage d’actionneurs pneumatiques permet de moduler facilement les efforts de serrage,
indépendamment de la fermeture du préhenseur.
L’étude suivante concerne un manipulateur à muscles artificiels développé au sein des équipes de recherche LGMT et LESIA
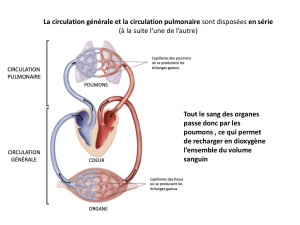
de l'INSA de Toulouse. Les photographies 1 et 2 présentent le manipulateur à structure anthropomorphique à 7 degrés de
liberté activés par des paires de muscles artificiels montés en opposition.

MPSI/PCSI TD n°5 SLCI Pôle Kerichen-Vauban
Page 2/7
La cinématique du robot est schématisée sur la figure 1.
Figure 1 : schéma cinématique du manipulateur
COMMANDE DE L’ACTIONNEUR
Le modulateur de pression qui apparaît sur la figure 2 a été dimensionné pour satisfaire la condition de vitesse de
l’actionneur.
Figure 2 : architecture d’un actionneur à muscle
On ne s’intéresse ici qu’à l’activation de la première liaison du bras manipulateur (paramètre
θ
).
Le couple de réaction engendré sur le bras par le moteur d’activation de la seconde liaison (paramètre
ϕ
) est alors considéré
comme un couple perturbateur extérieur ext C . Pour simplifier le problème, nous supposerons que ext C est négligeable devant
le couple moteur
m
C engendré par les muscles artificiels.
• Le principe fondamental de la dynamique appliqué au bras fournit alors l’équation :
)(.)()( tItCtC
eextm
θ
&&
=− où e I est l’inertie du bras selon l’axe de rotation de la liaison
2
.5,0 mkgI
e
=

MPSI/PCSI TD n°5 SLCI Pôle Kerichen-Vauban
Page 3/7
• m C est le couple moteur qui est désormais modélisé par l’équation suivante :
)(.)(.))()(()(
7521.4
tKtKtPtPKtC
m
θθ
&
−−−=
avec barmNK /.4
4
= , radmNK /.5
5
= et radsmNK /..8,0
7
=
• La réponse du modulateur de pression à une tension U de 1 V est fournie par le constructeur sur la figure 1 de
l’annexe 1.
• La tension de commande U du modulateur est élaborée à partir de l’écart entre la position angulaire souhaitée
∗
θ
et
la position angulaire effective
θ
par une loi de commande de transfert
p
K
U
pH
C
C
c
.1
)(
τθθ +
=
−∗
= .
Dans toute la suite du problème, l’écart de pression entre les deux muscles
21
PP − sera noté
P
∆
.
PARTIE 1 : MODELISATION
L’objectif de cette partie est d’établir le schéma bloc ainsi que la fonction transfert du système asservi d’entrée )(p
∗
θ
et de
réponse )(p
θ
.
1. Compléter le schéma bloc de la figure 2 de l’annexe 1 en fonction de
4
K ,
5
K ,
7
K et
e
I . Justifier chaque bloc.
Indiquer les grandeurs physiques ainsi que leurs unités.
2. Déterminer littéralement le rapport
)( )( pPp ∆
θ
.
3. En vous aidant de la figure 1 de l’annexe 1, déterminer graphiquement l’ordre et les paramètres caractéristiques de la
fonction transfert du modulateur de pression :
)( )(
)( pU pP pH
m
∆
= .
4. Compléter le schéma bloc de la figure 3 de l’annexe 2. Justifier chaque bloc. Indiquer les grandeurs physiques ainsi
que leurs unités.
5. Déterminer littéralement la fonction transfert du système complet :
)( )(
)( p
p
pH ∗ =
θ
θ
en fonction de
4
K ,
5
K ,
7
K ,
e
I ,
C
K ,
C
τ ainsi que
m
K et
m
τ déterminés au 3.
6. Les constantes de temps
m
τ et
C
τ sont très faibles, on peut donc considérer que les fonctions de transferts )(pH
m
et )(pH
c
sont modélisables par leurs gains statiques seuls. En prenant en compte cette hypothèse, Mettre
)( )(
)( p
p
pH ∗ =
θ
θ
sous sa forme canonique, déterminer les paramètres caractéristiques de )(pH en fonction de
4
K ,
5
K ,
7
K ,
e
I ,
m
K et
C
K .

MPSI/PCSI TD n°5 SLCI Pôle Kerichen-Vauban
Page 4/7
PARTIE 2 : ETUDE DU COMPORTEMENT
On prendra pour fonction de transfert dans la suite du sujet :
C475
2
e
C4
*KK25.0pKKpI KK25.0
)p( )p( +++
=
θ
θ
On souhaite amener le bras du robot à la position angulaire
°
=
30
θ
. La position initiale du bras est
°
=
0
θ
.
1. Déterminer le gain statique
C
K permettant d’assurer une erreur statique inférieur à 10%.
2. Pour valeur
C
K =45, déterminer le temps de réponse à 95% du système à l’aide de la figure 4 de l’annexe 2.
3. Tracer l’évolution de la position angulaire
)(t
θ
avec le plus grand soin en faisant apparaître l’erreur statique, le temps
de réponse à 95% ainsi que les différentes tangentes et / ou asymptotes éventuelles.
4. Conclure sur le comportement du robot. Quelles améliorations pourraient être apportées au système ?

MPSI/PCSI TD n°5 SLCI Pôle Kerichen-Vauban
Page 5/7
ANNEXE 1
0
0,05
0,1
0,15
0,2
0,25
0,3
0 0,05 0,1 0,15 0,2 0,25 0,3 0,35
Ecart de pression
∆P pour une tension d'alimentation U=1V
∆P (bar)
t (s)
Figure 1 : Réponse du modulateur de pression
-
+
P(p) ∆ θ (p)
Figure 2 : Schéma bloc partiel