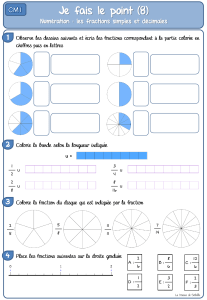
dx - fractions rationnelles

DX - FRACTIONS RATIONNELLES
On désigne une fraction rationnelle non nulle irréductible à coefficients réels par
f(x) = P(x)
Q(x).
où Pet Qsont des polynômes de degrés respectifs pet q. On note
deg f= deg P−deg Q .
Si αest un pôle de fd’ordre n, c’est-à-dire une racine de Qd’ordre n, on notera R(x)le quotient de
Q(x)par (x−α)n. Si de plus αn’est pas réel, alors on notera
(x−α)(x−¯α) = x2+ux +v
qui est un polynôme à coefficients réels, et S(x)sera le quotient de Q(x)par (x2+ux +v)n.
I Théorème de décomposition
Le théorème de décomposition des fractions rationnelles en éléments simples sur C, dit que f(x)s’écrit
comme somme de différentes parties :
(1) une partie polynomiale de degré p−q, si p≥q
a0xp−q+a1xp−q−1+···+ap−q
(2) pour tout pôle αd’ordre n, une partie polaire de la forme
b0
(x−α)n+b1 (x−α)n−1+···+bn−1 x−α,
cette décomposition étant unique.
Dans le cas de la décomposition sur R, on a encore (1), on a aussi (2) pour tout pôle réel, auxquelles
s’ajoutent dans le cas des pôles αnon réels des sommes du type
(3) c0x+d0
(x2+ux +v)n+c1x+d1 (x2+ux +v)n−1+···+cn−1x+dn−1 x2+ux +v.
Là encore, la décomposition est unique.
Exemple 1
x9+x
(x−1)3(x2+ 1)2(x+ 2)

DX 2
– On a p= 9 et q= 8. Il y a une partie polynomiale de degré p−q= 1.
– Il y a un pôle réel d’ordre 3:1
– un pôle réel d’ordre 1:−2
– deux pôles non réels conjugués d’ordre 2:iet −i.
La décomposition sur Csera de la forme
(ax +b) + c
(x−1)3+d (x−1)2+e x−1+g x+ 2+h (x−i)2+k x−i+ℓ (x+i)2+m x+i
Sur Rles deux dernières sommes seront remplacées par
nx +r
(x2+ 1)2+sx +t x2+ 1 .
Les méthodes qui suivent donnent des moyens pour déterminer les coefficients qui apparaissent dans
la décomposition.
II Méthodes globales
A) Par identification
On écrit la décomposition cherchée sous forme littérale. On réduit au même dénominateur, et l’on
identifie les numérateurs, ce qui fournit un système d’équations linéaires dont les inconnues sont les
coefficients.
Exemple 2
x2−3
(x−1)2(x+ 1) =a (x−1)2+b x−1+c x+ 1
=(b+c)x2+ (a−2c)x+a−b+c
(x−1)2(x+ 1) .
Il reste à résoudre le système
b+c= 1
a−2c= 0
a−b+c=−3
et l’on obtient (a, b, c) = (−1,3
2,−1 2).
B) En donnant à xdes valeurs numériques
La décomposition étant écrite sous forme littérale, on donne à xdes valeurs judicieuses, par exemple
celles qui annulent le numérateur. Il en faut au moins autant que de coefficients à déterminer. On
obtient là encore un système que l’on résout. On peut aussi calculer
lim
x→∞ xsf(x)

DX 3
pour une valeur convenable de s.
Exemple 3
x2−2x−3
(x−1)2(x−2) =a (x−1)2+b x−1+c x−2.
On effectue les calculs suivants :
f(−1) = 0 = a
4−b 2−c 3
f(3) = 0 = a
4+b 2+c
lim
x→+∞xf(x) = 1 = b+c
On obtient facilement (a, b, c) = (4,4,−3)
Remarque : ces méthodes ne sont intéressantes que si le nombre de coefficients à déterminer est petit.
III Réduction du nombre de coefficients à déterminer
A) Cas des fractions paires ou impaires
Pour de telles fractions, si αest un pôle d’ordre n, il en est de même de −α.
– Le coefficient de (x+α)−pest, au signe près, celui de (x−α)−p.
– La partie polynomiale a même parité que f.
– Si 0est un pôle, la partie polaire relative à 0a même parité que f.
En pratique, on écrit la fraction décomposée sous forme littérale. On calcule f(−x) si fest paire et
−f(−x)si fest impaire, et l’on identifie le développement obtenu avec celui de f(x), ce qui fait ap-
paraître les termes égaux et les termes nuls.
Exemple 4
x6+ 2
(x2+ 1)(x2−16) =ax2+bx +c+d x−4+e x+ 4 +gx +h x2+ 1 .
comme fest paire, on calcule f(−x)
f(x) = f(−x) = ax2−bx +c−d
x+ 4 −e x−4+−gx +h x2+ 1 .
On en déduit que b=g= 0 et que d=−e. Donc
f(x) = ax2+c+d
x−4−d x+ 4 +h x2+ 1 .

DX 4
B) Fractions vérifiant une relation du type f(λx) = µf (x)
Si αest un pôle d’ordre n, il en est de même de λα, et les coefficients des décompositions polaires
relatives à ces pôles sont liés par des relations qui proviennent de l’unicité de la décomposition. La
méthode est analogue au III A).
Exemple 5
f(x) = x6
x5−1.
Posons z=e2iπ/5: c’est une racine 5−ième de l’unité. On a
f(zkx) = zkf(x).
Si l’on pose
f(x) = ax +b+c
x−1+d x−z+e x−z2+g x−z3+h x−z4,
on écrit le début de la décomposition de z−kf(zkx). Par identification on a
f(x) = z−kf(zkx) = ax +z−kb+cz−2k
x−z−k+···.
on en déduit b= 0, et en faisant varier k, sachant que z−1=z4, on obtient
k= 1 : z−k=z4donc h=cz−2=cz3
k= 2 : z−k=z3donc g=cz−4=cz
k= 3 : z−k=z2donc e=cz−6=cz4
k= 4 : z−k=zdonc e=cz−8=cz2.
C) Fractions vérifiant des relations du type f(x−λ) = µf (x)ou f(λ−x) = µf(x)
Les coefficients des décompositions polaires relatives à αet α−λou λ−αsont liés. Même méthode
qu’en A et B.
Exemple 6
1
(x2−3x+ 2)2=a (x−1)2+b x−1+c (x−2)2+d x−2.
Or
f(3 −x) = f(x) = a
(2 −x)2+b 2−x+···.
d’où a=cet b=−d.
D) Cas de la décomposition dans Cd’une fraction à coefficients réels
•Les coefficients de la partie polynomiale sont réels.

DX 5
•Les coefficients de la partie polaire relative à un pôle réel sont réels.
•Si αest un pôle non réel d’ordre p, alors ¯αen est un aussi.
Le coefficient de 1
(x−α)pest le conjugué de celui de 1 (x−¯α)p. Cela vient du fait que f(x) = f(x).
Exemple 7 x−1
x2+ 1 =a x−i+¯a x+i.
IV Détermination des coefficients par pôle
A) Recherche de la partie polynomiale lorsque p≥q
On effectue la division euclidienne de Ppar Q: le quotient est la partie polynomiale cherchée.
Remarque : le coefficient de xp−qest le rapport des termes de plus haut degré. En particulier si p=q,
la partie polynomiale se réduit à une constante qui est le rapport des termes de plus haut degré.
Si l’on a
P=UQ +V
avec deg(V)<deg(Q)on obtient donc
P
Q=U+V Q.
On pourra continuer la décomposition aussi bien en utilisant la fraction P/Q qu’en utilisant V /Q.
En fait Pest en général plus simple que Vbien que de degré plus élevé, et il est souvent préférable
d’utiliser P/Q, ce qui évite d’ailleurs de calculer V.
On peut déterminer ad’une autre manière, en effectuant le développement limité de fà l’infini. On
met tout d’abord xpen facteur dans P(x)et xqdans Q(x). On a donc
P(x)
Q(x)=xp−qH(x),
où Hest une fraction rationnelle. On pose alors x= 1/u, et l’on cherche le développement limité de
H(1/u)à l’ordre p−qen 0. En multipliant le résultat obtenu par xp−qon obtient, en revenant en x,
le quotient cherché.
Exemple 8
f(x) = x5+ 2x−1
(x−1)3(x+ 1) .
a) En développant le dénominateur
Q(x) = (x−1)3(x+ 1) = (x−1)2(x2−1) = (x2−2x+ 1)(x2−1) = x4−2x3+ 2x−1,