Méthode des moindres carrés - Univ

CUEEP Département Mathématiques T902 : Méthode des moindres carrés p1/16
Méthode des moindres carrés
Situation
Le lancer de poids
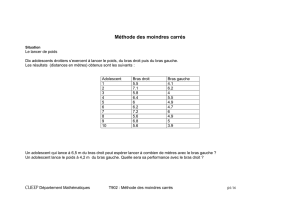
Dix adolescents droitiers s’exercent à lancer le poids, du bras droit puis du bras gauche.
Les résultats (distances en mètres) obtenus sont les suivants :
Adolescent Bras droit Bras gauche
1 5.5 4.1
2 7.1 6.2
3 5.8 4
4 6.4 5.5
5 6 4.9
6 6.2 4.7
7 7.2 6
8 5.6 4.9
9 6.8 5
10 5.6 3.9
Un adolescent qui lance à 6,5 m du bras droit peut espérer lancer à combien de mètres avec le bras gauche ?
Un adolescent lance le poids à 4,2 m du bras gauche. Quelle sera sa performance avec le bras droit ?

CUEEP Département Mathématiques T902 : Méthode des moindres carrés p2/16
Méthode
Ajustement linéaire par la méthode des moindres carrés
Soit une série statistique double représentée par un nuage de n points Mi (xi ; yi) et une droite D d’équation y = ax + b.
La méthode de Mayer nous a permis de trouver une équation de droite mais ne nous a pas permis de calculer les écarts des points à la droite
ainsi définie. Nous proposons une autre méthode qui va permettre de mesurer ses écarts.
L’ajustement de la droite D au nuage de points sera d’autant meilleur que les points Mi seront les plus rapprochés de la droite D.
Pour trouver l’équation de D on devra chercher la somme minimale des distances des points à la droite D
Comment mesurer cette distance ?
La solution qui au départ paraît la plus naturelle car c’est la « vraie distance » du
point à la droite n’est pas retenue par les statisticiens pour différentes raisons.
Cette méthode est géométriquement facile mais très compliquée à faire par le calcul.
D’autre part si les unités n’étaient pas les mêmes comme dans cet exemple, cela
n’aurait aucun sens.
Une deuxième solution aurait été d’additionner les deux distances (horizontale et verticale) du
point à la droite.
Pour les mêmes raisons d’unités, on ne peut pas utiliser cette méthode.
De plus ce qui nous intéresse est lié à un problème orienté. On cherche l’influence d’une variable
sur l’autre. Ces deux variables ne jouent pas un rôle symétrique.
Par exemple, pour un droitier connaissant ses performances du bras droit peut-on pronostiquer
ses performances du bras gauche ?
De même pour un gaucher peut-on pronostiquer ses performances du bras droit connaissant
celles du bras gauche ?

CUEEP Département Mathématiques T902 : Méthode des moindres carrés p3/16
Finalement on est ramené à calculer les distances orientées, on compare la valeur calculée à la
valeur observée en calculant l’écart entre ces deux valeurs. Si le point est au dessus de la
droite l’écart aura une valeur négative, s’il est en dessous, l’écart aura une valeur positive.
Deux choix restaient encore possible : additionner les valeurs absolues ou les carrés de ces écarts .Là encore le 1er choix qui consisterait à
prendre les valeurs absolues et à les sommer, tout en étant licite, se révèle difficile à calculer.
Par contre le calcul des carrés conduira à un calcul algébrique utilisant uniquement l’algèbre du second degré qui se révèlera facile à mettre en
œuvre ( cf : calcul de l’écart type dans les statistiques à une variable)

CUEEP Département Mathématiques T902 : Méthode des moindres carrés p4/16
La droite d’ajustement a pour équation générale y = ax + b.
Le point Mi a comme coordonnée i
x et i y
Le point Pi est le point de la droite à l’abscisse xi. Son ordonnée est baxi+
La distance entre Mi et Pi est égale à )( baxy ii +−
Quand le point Mi est au dessus de la droite l’expression yi –(axi + b) est
positive.
Quand le point Mi est en dessous de la droite l’expression yi –(axi + b) est
négative.
Comme pour le calcul de l’écart type on fait la somme des carrés des
distances et il faut déterminer les coefficients a et b pour que cette somme soit
minimale.
On note cette somme
[]
²)(
∑
+− baxy ii
C’est pour cela que cette méthode s’appelle « la méthode des moindres
carrés.
Mi
Pi
xi
yi
axi+b
01
1
Mi
Pi
xi
yi
axi+b

CUEEP Département Mathématiques T902 : Méthode des moindres carrés p5/16
Plan de travail
Animation
L’activité proposée est la suivante :
Un nuage de points est tracé à l’écran, vous devez actionner une droite par rotation et déplacement afin que cette droite passe au mieux parmi
le nuage. La somme des carrés des écarts des points à la droite s’affiche ainsi que la somme minimale.
Pour déplacer la droite vous avez le choix entre :
un déplacement manuel d’un point P de la droite à l’aide de la petite main ! et une rotation à l’aide du symbole !
une modification des coefficients a et b avec les touches + et - .
Animation
Utilisation du tableur
Calcul du carré des écarts
Dans le classeur1 les données du problème sont rentrées, en fixant une valeur de a pour le coefficient de la droite, et en faisant varier le
coefficient b le tableau fournit automatiquement la somme des carrés des écarts, le graphique de la somme en fonction de b s’affiche ainsi que
la formule associée.
Donner à a la valeur 1 et faites varier b de -2 à -0,5 avec un pas de 0,05.
Quelle est la nature de la courbe obtenue ? (droite, parabole, hyperbole, autre..)
ATTENTION : il faut que toute la colonne soit remplie pour que la courbe et l’équation s’affichent correctement.