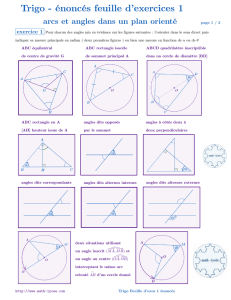
1 1. Exprimer ces angles en radians ( rad )

1
1. Exprimer ces angles en radians ( rad ) et en π radians ( π rad )
a) 300° b) 15° c) 130° d) e) f) 90°
g) 270° h) 180° i) j) k) l)
2. Exprimer ces angles en degrés
a) b) c) d) e) f) 2 rad g) π rad
h) 5,5 rad i) -3 rad j) 0,5 rad k) l) -2 rad m)
3. Convertir en fonction de l’unité de mesure demandée
a) b) 60° = ? tour c) 2 tours = ? degrés d) 2 tours = ? rad
e) 8π rad = ? tours f) 3π rad = ? tours g) h)
i) j) 34 rad = ? tours k) 900° = ? tours l) 5 tours/s = ? rad/s
4. Une roue de bicyclette tourne à une vitesse de 180 tours/minute .
a) Exprimer la vitesse en radians/seconde
b) Quelle distance la roue parcourt-elle en 30 minutes si le rayon de la roue est de 40 cm ?
5. Les angles suivants ( en radians ) sont exprimés en multiples de . Exprime ces angles en degrés sans
utiliser la calculatrice .
a) b) c) d) e) f) g)
6. Les angles suivants ( en radians ) sont exprimés en multiples de . Exprime ces angles en degrés ( ne
pas utiliser la calculatrice ) .
a) b) c) d) e) f) g)
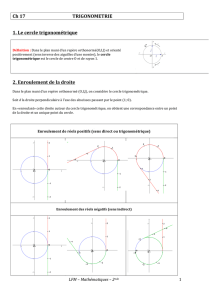
7. Déterminer la longueur de l’arc intercepté par un angle au centre dans le cercle trigonométrique de
rayon = 1 cm si l’angle est de :
a) 3 rad b) 45° c) 2π rad d) 4,5 rad e) 135° f) 270°
8. Déterminer la longueur de l’arc intercepté par l’angle au centre en tenant compte de la mesure du rayon.
a) θ = r = 3 cm b) θ = π rad r = 21 cm c) θ = r = 5,2 cm
d) θ = 52° r = 4 km e) θ = 0,9 rad r = 11 cm f) θ = 72° r = 1 km
g) θ = r = 2 m h)

2
9. Déterminer sans calculatrice la mesure de l’angle au centre ( en degrés ) si cet angle définit un arc de
cercle dont la longueur est de :
a) unités b) unités c) unités d) unités e)
10. Déterminer la mesure de l’angle au centre ( en radians ) d’un cercle de rayon r qui intercepte un arc de
longueur l tels que :
a) r = 7 cm et l = 5 cm c) r = 9 cm et l = 15 cm
b) r = 4 cm et l = 6 cm d) r = 8 cm et l = 48 cm
11. Calculer la longueur de l’arc ( en ) :
a ) m b) m c) m
12. Dans quel quadrant du plan cartésien se situent les points trigonométriques suivants :
a) b) c) d) e) P(3) f) P(-5) g) P(33)
h) P(12) i) j) k) l)
m) P(400°) n) P( -120°) o) p) q)
r) s) t) u) v) w)
13. Déterminer les points du cercle trigonométriques dont :
a) b) c) d)
e) f) g) h)
14. Déterminer la valeur exacte de ces expressions ( se référer uniquement au cercle trigonométrique )
a) b) c) d) e) f)
g) h) i) j) k)
l) m) n) o)
ne pas
utiliser la
calculatrice
!
30
0
A
B
C
D
E
F
6 cm
4 cm
8 cm
ne pas
utiliser la
calculatrice
!

3
15. Ces points appartiennent-ils au cercle trigonométrique ?
a) b) c) d)
16. Déterminer les coordonnées exactes des points trigonométriques suivants
Rappel : coordonnées du point P :
( Ces coordonnées représentent aussi les composantes horizontale et verticale du vecteur )
a) b) c) P d) e) P( ) f) P(3) g)
h) i) j) P(0) k) l) m) P (175°)
n) o) p) q) r) s)
17. Déterminer l’angle au centre en degrés de 2 façons :
10 : à l’aide des coordonnées du numéro 16 ( l’angle d’un triangle rectangle )
20 : à l’aide de la formule :
a) b) c) P(3) d)
18. Déterminer les 2 valeurs possibles d’angles x ( en degrés ) si :
a) b) c) d) e)
f)
19. Déterminer les 2 valeurs possibles d’angles t ( en degrés et en radians ) si :
a) b) c) d) e)
f)
20. Quelle point trigonométrique a la même abscisse que :
a) b) c) P(2,87) d) P(24) e) P(75) f) g) P(100)
21. Quelle point trigonométrique a la même ordonnée que :
a) P(π) b) c) P(3) d) P(20) e) P(120) f) P(1)

4
22. Voici des coordonnées ( abscisse, ordonnée) de points P du cercle trigonométrique.( rayon égal à
1 unité ). Déterminer les valeurs possibles de la coordonnée manquante du point trigonométrique P.
a) P(0, y) b) c) P( -0,4 , y ) d) e) f) P ( x , )
g) h)
23. Un angle au centre de θ rad intercepte sur
un cercle de r cm de rayon un arc d’une
longueur de L cm . Compléter ce tableau :
24. Un plan cartésien est superposé à l’écran radar ( cercle trigonométrique ) d’un contrôleur aérien ;
l’origine du plan cartésien correspond à la position de la tour de contrôle . 2 avions sont situés aux
angles suivants (orientation ) : et . Quelle distance sépare les 2 avions s’ils se trouvent
à 1 km de la tour ?
25. La station spatiale internationale est à une altitude moyenne de 347 km . La Terre a un rayon moyen de
6371 km .
a) Déterminer le rayon moyen de l’orbite de la station .
b) La station prend 91 minutes à faire un tour complet . À quelle vitesse se déplace-t-elle
1) en radians/sec ?
2) en mètres/sec
3) en km/heure ?
L
r
θ
a
3
5
b
1,5
10
5
c
d
8
2,5
4,9
e
4
21
2
f

5
26. Déterminer , en radians , la valeur de l’angle θ .
Diamètre du cercle : 4,9 cm Aire du cercle : 95,03 cm2
27. Soit le cercle dont l’angle au centre est de rad .
Cet angle intercepte un arc de 8,25 m .
Déterminer l’aire du cercle .
28. a) Déterminer la mesure de l’arc AB ( en m ) b) Déterminer la mesure de l’arc AB ( en cm )
si l’aire du cercle est de 400 m2 et que si l’aire du cercle est de 300 cm2 et que
l’angle θ est de 75°
29. Localise le point P(t) sur le cercle trigonométrique si
a) b) c) d) e) f)
AB
o
AB
o
0
0
a) b)
A
B
o
L= 8,25 m
A
B
A
B
o