N°44-Stage+Thèse_LIMSI_L.Pastur+M.Jaharri_advection

PROPOSITION DE SUJET DE STAGE ET DE THESE
Advection chaotique de la chaleur dans un écoulement fluide modèle
Laboratoire : LIMSI
Responsables du stage : Luc Pastur, Mojtaba Jaharri
E-mail : [email protected]
Téléphone : 01 69 85 80 77
Projet : Stage M2 + Thèse (SMeMAG)
L’analyse lagrangienne d’un écoulement fluide consiste à « étiqueter » un certain nombre de traceurs,
passifs ou non, et d’en suivre les trajectoires au cours du temps, compte-tenu du champ de vecteurs qui
pilote leur évolution. Cette analyse permet de révéler la structure topologique de l’écoulement : régions
dynamiquement importantes, attractives ou répulsives, barrières infranchissables au sein du fluide ou zones
de mélange, etc. Par exemple, les trajectoires des particules fluides (traceurs passifs) sont directement pilotées
par le champ de vitesse, et lorsque l’écoulement est incompressible, sa description (lagrangienne) est analogue
à celle d’un système dynamique conservatif, évoluant dans un espace des états de la dimension de l’espace
physique (2D ou 3D) [1]. En effet, on peut formellement écrire :
Ẋ = U(X, t),
div U = 0,
où X est la position de la particule fluide et U le champ de vitesse à divergence nulle dans le cas d’un écoulement incompressible. Lorsque l’écoulement est bi-dimensionnel, le système présente de plus une structure
hamiltonienne où la fonction courant ψ fait office d’Hamiltonien pour le système.
On peut sur le même principe définir une « particule de chaleur » par analogie avec la particule fluide. Le
système dynamique équivalent, du type Ẋ = u(X, t), fait un alors intervenir un champ de vitesse u qui n’est
plus à divergence nulle, même si le champ de vitesse total U l’est toujours. Le système dynamique équivalent
est maintenant dissipatif [2]. Dans un tel système, un grand nombre de particules prises au hasard dans
l’écoulement tendront asymptotiquement vers un même attracteur dont la dimension peut être fractale si
la dynamique est chaotique. C’est ce type de situation que nous souhaitons étudier dans ce projet exploratoire.
La configuration choisie pour cette étude est une cavité ouverte 3D différentiellement chauffée, soumise à
la gravité, dans les conditions de Boussinesq. A bas nombres de Reynolds et de Rayleigh, une recirculation
principale, stationnaire, est engendrée par l’écoulement externe, qui se comporte comme un « tapis roulant »
pour le fluide intra-cavitaire, tandis qu’un écoulement de convection est induit par les bords amont et aval
portés à des températures différentes. Si le bord amont est plus froid que le bord aval, l’écoulement de
convection naturelle s’établit à contre-courant de la recirculation principale. On s’attend à ce que le mélange
présente dans ce cas une topologie non triviale. Au-delà d’une valeur critique du nombre de Reynolds, des
instabilités centrifuges peuvent se développer sur l’écoulement de recirculation principale [4]. Les structures
1
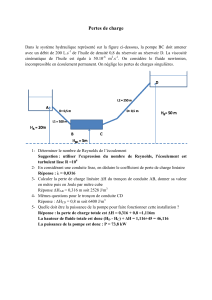
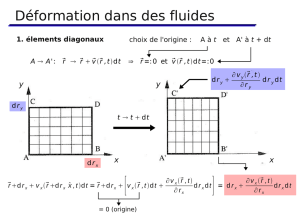
Figure 1 – Exemple de la topologie de mélange d’un écoulement de cavité différentiellement chauffée, d’après
[3]. Les points bleus et rouges sont des particules fluides initialement ensemencées autour des points verts,
puis transportées par le flot en temps direct (rouge) ou rétrograde (bleu).
de vorticité engendrées sont toujours stationnaires à saturation, mais la topologie du champ de vitesse est
plus complexe, ce qui devrait avoir des conséquences drastiques sur le mélange. A plus haut nombre de
Reynolds encore, le « tapis roulant » fluide, au-dessus de la cavité, perd à son tour sa stabilité et exhibe des
oscillations auro-entretenues intenses. La dynamique est alors instationnaire périodique.
Dans le cadre du stage, nous étudierons le mélange dans l’état stationnaire de plus haute symétrie, à bas
nombres de Reynolds et de Rayleigh, sous Fluent. Les régimes dynamiques plus complexes seront abordés
dans la cadre d’une thèse : les champs de vitesse et de température seront alors simulés sous SUNFLUIDH
(code natif LIMSI parallélisé), dans lequel le doctorant devra implémeter un module de suivi lagrangien.
Références
[1] J.M. Ottino, “The Kinematics of Mixing : Stretching, Chaos, and Transport”, Cambridge University
Press, Cambridge, England (2004).
[2] M. Speetjens, “A generalised Lagrangian formalism for thermal analysis of laminar convective heat
transfer”, Int. J. Therm. Sciences 61, pp 79-93 (2012).
[3] L. Otesky, “Transition vers le chaos en convection naturelle confinée : descriptions lagrangienne et
eulérienne”, Thèse de Doctorat (2015).
[4] C. Douay, “Etude expérimentale paramétrique des propriétés et transitions de l’écoulement intracavitaire en cavité ouverte”, Thèse de Doctorat (2015).
2