exp(- x)

FONCTION EXPONENTIELLE ET EQUATION DIFFERENTIELLE.
I LA FONCTION EXPONENTIELLE
1° Généralités
Il existe de nombreuses situations en sciences expérimentales et en sciences économiques dans lesquelles des
phénomènes peuvent être modélisés par des équations du type y' = k y, où y désigne une fonction définie et
dérivable sur un intervalle I.
Résoudre sur I l’équation différentielle que l’on note y' = k y, c’est rechercher toutes les fonctions f dérivables sur
l’intervalle I qui vérifie la relation : f '(x) = k f(x) pour tout x de I
Si de plus, le problème considéré impose aux fonctions f cherchées des conditions qui se traduisent par une égalité
de la forme f(x0) = y0 où x0 et y0 sont deux réels donnés avec x0 élément de I, on dit que l’on résout l’équation
différentielle avec condition initiale (à savoir f(x0) = y0) que l’on note alors :{ y' = k y;y(x0) = y0
2° Cas particulier : équation différentielle y' = y, y(0) = 1. Fonction exponentielle
a) Définition
Il existe une fonction f, dérivable sur I; R, solution de l'équation différentielle Y '= Y et telle que f(0) = 1 que l'on
appelle la fonction exponentielle.
Existence de f :
La méthode d'Euler suggère d'étudier les suites
Error!
et
Error!
.
On admet provisoirement que pour tout réel x ces deux suites convergent vers la même limite et on note
provisoirement exp (x).
b) Démonstration. Unicité de f
Démontrons d'abord que exp ne s'annule pas sur I; R .
Soit la fonction  définie sur I; R par  (x) = exp(x) exp(– x).  est dérivable sur I; R et
'(x) = exp'(x) exp(–x) – exp(x) exp'(– x) = 0.
La fonction  est constante sur I; R et égale à 1 car exp(0) = 1. donc (0) = 1
Donc pour tout réel x, exp(x) exp(– x) = 1.
Donc pour tout réel x, exp(x) 0
La fonction exp ne s'annule donc pas sur I; R .
Démontrons maintenant l'unicité de la solution.
Soit f une solution de { y' = y;y(0) = 1
On définit h la fonction définie sur I; R par h(x) =
Error!
Remarque : f est bien définie sur I; R car la fonction exp est définie sur I; R et elle ne s'annule pas sur I; R.
On va démontrer que la fonction h est constante sur I; R et pour tout réel x h(x) = 1 ce qui démontrera que les
fonction f et exp sont identiques.
h est le quotient de deux fonctions dérivables sur I; R et h est définie sur I; R donc h est dérivable sur I; R.
h '(x) =
Error!
=
Error!
= 0.
En effet pour tout réel x f '(x) = f(x) et exp '(x) = exp(x).
La fonction h a donc sa fonction dérivée nulle sur l'intervalle I; R elle est donc constante sur I; R.
Pour tout réel x h(x) =h(0) =
Error!
=
Error!
= 1.
On a donc bien pour tout réel x,
Error!
= 1 c'est à dire f(x) = exp(x).

2° Propriété
La fonction exponentielle est strictement positive sur I; R.
Démonstration
On démontre maintenant, par l'absurde, que la fonction exp est strictement positive.
Supposons que la fonction exp ne soit pas strictement positive.
exp strictement positive signifie que, pour tout réel x, exp(x) >0
exp non strictement positive signifie qu'il existe un réel x, tel que exp(x) 0.
Supposons donc qu'il existe un réel x0 tel que exp(x0) 0.
On a alors exp(x0) 0 < exp(0).
Comme la fonction exp est dérivable sur I; R, elle est continue sur I; R.
On peut donc appliquer le théorème des valeurs intermédiaires sur l'intervalle de bornes x0 et 0 ([0 ; x0] ou [x0 ; 0])
à la fonction exp : il existe donc une solution à l'équation exp(x) = 0 dans l'intervalle [0 ; x0] (ou [x0 ; 0]).
Ceci est impossible puisqu'on a démontré que exp ne s'annule jamais sur I; R.
Donc il n'existe pas de réel x0 tel que exp(x0) 0 c'est à dire que pour tout réel x, exp(x) > 0
Remarque : si f est continue sur un intervalle I et si f ne s'annule pas sur cet intervalle alors f garde un signe
constant sur l'intervalle I.
3° Propriété ("caractéristique" de la fonction exp)
Pour tous nombres réels a et b, exp (a + b) = exp(a) exp(b).
Remarque On a vu que pour tout réel x exp(x) exp(– x) = 1 = exp(x + (– x))
Démonstration
Soit la fonction g définie sur I; R par g(x) = exp(a+ b – x) exp(x) où a et b sont des nombres réels.
g est dérivable sur l'intervalle I; R, et on a pour tout réel x :
g '(x) = – exp(a + b – x) exp (x) + exp(a + b – x) exp '(x) = 0
car exp '(x) = exp(x)
La fonction g est donc constante sur l'intervalle I; R
g(b) = exp (a + b – a) exp (b) = exp(a) exp(b)
g(0) = exp(a + b – 0) exp (0) = exp(a + b)
Donc, pour tout réel b, g(b) = g(0) c'est à dire : exp(a) exp(b) = exp (a + b)
La propriété est "caractéristique" de la fonction exp
Error!
caractérise la fonction exp.
C'est à dire que si une fonction f vérifie
Error!
.
alors cette fonction est la fonction exp.
Démonstration Soit f une fonction vérifiant
Error!
Pour tout réel a, f(a + 0) = f(a) f(0) donc pour tout réel a : f(a) (1 – f(0)) = 0
On sait que f '(0) 0, on peut dire que la fonction f n'est pas constante sur I et donc qu'il existe un réel a tel que
f(a) 0. On peut donc conclure que f(0) = 1
Pour tout réel a on pose ga la fonction définie sur I; R par : ga(x) = f(a + x) = f(a) f(x).
ga est la composée de deux fonctions dérivables sur I; R elle est donc dérivable sur I; R
on peut alors calculer la fonction dérivable de g de deux manières différentes
En utilisant l'égalité : ga(x) = f(a + x)
Pour tout réel x on a donc :
Pour tout réel x on a ga(x) = f(a + x) donc ga '(x) = f '(a + x) (x + a)'
En utilisant l'égalité : ga(x) = f(a) f(x)
Pour tout réel x on a :ga(x) = f(a) f(x) donc ga '(x) = f(a) f '(x)
En comparant les deux calculs on peut dire que :
Pour tout réel x f '(a + x) = f (a) f '(x).
Pour x = 0 on obtient (pour tout réel a): f '(a + 0) = f(a) f '(0) c'est à dire f '(a) = f(a) (car f '(0) = 1)
On peut dire que pour tout réel a, f '(a) = f(a)? f vérifie donc : { f(0) = 1;f ' = f c'est donc la fonction exp

II NOTATION ex
1° Cas de x I;Q
Le nombre réel exp(l) se note e.
• Tout d'abord, on montre, par récurrence, que, pour tout nombre n entier naturel, on a :
« exp(n) = (exp(1))n. »
Initialisation
On a : exp(0) = 1 et (exp(1))0 = 1
La propriété est donc vraie pour n = 0
Hérédité
Considérons un entier k, on ait exp(k) = exp(1))k.
On a vu qu'alors :
exp((k + 1)) = exp(k) exp(1)= exp(1))k exp(1) = (exp(1))k+ 1 .
On a bien exp(k + 1) = (exp(1))k+1
Conclusion
La propriété est vérifiée pour n = 0.et elle est héréditaire donc pour tout nombre entier n exp(n) = (exp(1)n = en
• Pour tout entier relatif m on a : exp(m) = em
Si m I; N la propriété a été vérifié.
Si m = – n avec n I; N
Par définition, exp(1) = e et on a vu que, exp(n) exp(–n) = 1.
Donc exp(m) = exp(–n) =
Error!
=
Error!
= (exp(1)–n = (exp(1))m = em
• Pour tout nombre rationnel q : exp(q) = eq
Si q est un nombre rationnel, on peut écrire q = p a avec a =
Error!
, q entier strictement positif et p un entier
relatif. : exp(1) = exp(q a) = (exp(a))q.
On peut donc dire que : exp(a) = (exp(1))
Error!
exp(q) = exp(p a) = exp(a)p =
Error!
Error!
= (exp(1))
Error!
Soit exp(q) = (exp(1)q = eq
Donc, pour tout q élément de I;Q, exp(q) = eq .
2° Notation
• On étend cette propriété à I; R et on convient de noter ex le nombre exp(x) pour tout x élément de I; R.
Remarques Ainsi e
2
a un sens, c'est l'image de 2 par la fonction exp : x
Error!
ex .
On a aussi e0 = 1 ; el = e ; e–1 = 1 ; e
2
1
= e
3° Conséquences
Pour tous nombres réels a et b . ea+b = ea eb
e–a =
Error!
ea–b =
Error!
Pour tout nombre réel a et tout nombre rationnel r : era = (e°)r.
Exemples
ex+1 = ex e ; ex–2 = ex e2 ; e2x = (ex)2 ; e
2
x
= ex.
Remarque
Ne pas confondre e
b
a
et ( ) ea b ; ainsi e
2
x
= exp(x2) alors que (ex)2 = e2x.

III ETUDE DE LA FONCTION x
Error!
ex
D'après sa définition : solution de l'équation différentielle Y ' = Y et telle que f(0) = 1, la fonction x
Error!
ex est
dérivable sur I; R donc continue sur I; R, et égale à sa dérivée.
1° Variations
• x
Error!
ex est strictement croissante sur
Error!
.
Démonstration
On a (ex )' = ex et pour tout x ex > 0.
2° Limite en 0
lim;x  0
Error!
= 1
Démonstration
La fonction x
Error!
ex est dérivable en 0 donc son taux de variation
Error!
a pour limite en 0 le nombre dérivé de
x
Error!
ex en 0, soit :
Error!
Error!
= e0
3° limites en + et en –
Error!
ex = +
Error!
ex = 0
Démonstration
• Pour étudier la limite en + , on montre d'abord que, pour tout x,
ex x Soit la fonction f définie sur R par f (x) = ex – x.
f est dérivable sur I; R et f (x) = ex – 1.
Comme exp est croissante sur I; R et e0 = 1, on obtient le tableau de
variations de f ci-dessous.
Comme, pour tout x, f(x) > 0, on a ex > x et,
d'après un des théorèmes « des gendarmes », on a :
Error!
ex = +
.• Pour étudier la limite en – , on pose X = – x et on a ex = e–X =
Error!
. :
Error!
ex =
Error!
e–X =
Error!
Error!
= 0 car
Error!
eX = +
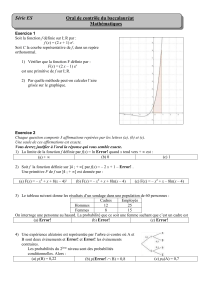
4° Tableau de variations de la fonction exp et représentation graphique
x
1
1
+
signe de f '
+
+
+
+
f
e
1
0
• La courbe représentative de la fonction : x
Error!
ex passe par les points de coordonnée (0 ; l) et (1 ; e).
• La tangente à la courbe représentative de la fonction : x
Error!
ex au point de coordonnées (0 ;1) a pour équation
y = x + 1. De plus, pour h « assez petit » : eh 1 + h.
• La courbe représentative de la fonction x
Error!
ex est au-dessus de l'axe des abscisses, qui est une droite
asymptote.
5° Conséquences
• Pour tout nombre réel x : ex > 0.
• Pour tous nombres réels x et y : ex = ey équivaut à x = y . ex > ey' équivaut à x > y.
Exemples
• e3x = ex+1 équivaut à 3x = x + 1.
• ex  1 équivaut à x  0.
• ex = 1 équivaut à x = 0.
6° Fonction eu(x)
Soit u une fonction définie sur un intervalle I.
Si u est dérivable sur I, alors la fonction x
Error!
eu(x) est dérivable sur I et sa dérivée est : x
Error!
u '(x) eu(x).
Démonstration
D'après le théorème de la dérivée d'une fonction composée, x
Error!
ex étant dérivable sur
Error!
et u dérivable sur
I, la fonction composée : x
Error!
u-(x)
Error!
eu(x) est dérivable sur I de dérivée x
Error!
u'(x) eu(x).
Exemple La fonction x
Error!
esin x est dérivable sur
Error!
de dérivée x –
Error!
cos x esin x.
7° Des limites fondamentales
Error!
Error!
= +
Error!
x ex = 0
Démonstration
• On a vu que, pour tout x, ex > x.
x
0
+
f '
–
+
f
1

Donc, pour tout x, ex/2
Error!
et, pour tout x 0,
e
Error!
2
Error!Error!
soit ex
Error!
donc
Error!
Error!
.
D'après un des « théorèmes des gendarmes », on obtient
Error!
Error!
= + .
• On a x ex =
Error!
.En posant X = – x, on a : x ex = –
Error!
.
Or
Error!
Error!
= 0 donc
Error!
x ex =
Error!
–
Error!
= 0
8° Autres limites
Pour tout nombre entier n strictement positif n
•
Error!
Error!
= + •
Error!
xn ex = 0.
Démonstration
• Comme ex > 0, - =
Error!
=
Error!Error!
.
On pose X =
Error!
on a
Error!
Error!
= + donc :
Error!
Error!
=
Error!
Error!Error!
= +
• On pose x = – X. On a : xn ex = (– X)n e–X, soit xn ex = (– 1)n
Error!
.
Donc
Error!
xn ex =
Error!
(– 1)n
Error!
= 0
Pour les limites en + et en – , on retiendra que « exp l'emporte sur x » .
III EQUATION DIFFERENTIELLE Y'= A Y+ B
1° Théorème
Soit a un nombre réel.
• Les fonctions solutions de l'équation différentielle Y '= a Y sont définies sur I; R par : f(x) = k eax où k est une
constante réelle.
• Soit (x0; y0) un couple de nombre réels.
L'équation différentielle Y '= a Y admet une solution unique sur R vérifiant les conditions initiales : y0 = f(x0).
Démonstration
La fonction x
Error!
eax est solution de l'équation Y ' = a Y.
Si f est une autre solution de l'équation Y ' = a Y
Soit g la fonction définie sur
Error!
par g(x) =
Error!
On a : g '(x) =
Error!
= 0 donc g est une fonction constante donc f est de la forme k eax
La condition y0 = f(x0) s'écrit y0 = k ea xo soit k =
Error!
.
Donc il existe un réel k unique et une unique fonction f solution de l'équation Y'= aY et vérifiant y0 = f (x0).
Exemple : Soit l'équation différentielle Y ' = – 2 Y.
Les solutions sont les fonctions x
Error!
ke–2x définies sur
Error!
. Parmi ces solutions, une seule vérifie f(1) = 3
f(1) = 3 équivaut à 3 = k e–2, soit k = 3 e2, donc f(x) = 3 e2 e–2x = 3e2–2x.
Remarque : Le réel a et le point A(xo ; yo) sont donnés.
Parmi les courbes représentatives des solutions de Y ' = a Y, il existe une seule courbe passant par A.