TD2 - Staps Lille 2

1
TD2 statistiques L5 S1 APA et ES (V.Bougault)
Exercice 6 : Les performances obtenues en athlétisme par les élèves d'une classe donnent lieu aux
notes suivantes :
Notes 5 6 7 8 9 10 11 12 13 14 15 16 17 18
Effectifs 1 1 2 1 2 1 4 3 4 2 1 2 1 0
a) Etablir l'histogramme et le polygone des fréquences cumulées de cette distribution de notes.
b) Calculer la moyenne, le mode, la médiane et l'écart-type de cette distribution.
On décide de regrouper ces notes dans des classes d'intervalle 3 et on choisit 5 comme centre d'une
classe.
c) Etablir l'histogramme de cette nouvelle distribution.
d) Calculer la moyenne, le mode, la médiane et l'écart-type de cette distribution.
Comparer ces nouveaux résultats aux précédents, commenter rapidement.
e) L'enseignant décide de monter toutes les notes ; il ajoute 2 points à chaque élève.
Quelle est la moyenne et quel est l'écart-type de cette nouvelle distribution ? (on ne procède pas à un
regroupement de classes)
Exercice 7 : Un entraîneur effectue une prise de performance des 20 athlètes dont il est responsable.
Il transforme ces performances en notes et obtient les résultats suivants :
5 ; 4 ; 6 ; 2 ; 3 ; 1 ; 7 ; 6 ; 3 ; 7 ; 7 ; 10 ; 3 ; 2 ; 6 ; 3 ; 10 ; 5 ; 3 ; 7
a) Etablir le tableau complet des effectifs, l'histogramme des fréquences et le polygone
cumulatif.
b) Quel est le mode de cette série ? La médiane ? La moyenne (arithmétique) ?
c)L'entraîneur retranche de chaque note la valeur de la moyenne et additionne alors les
résultats obtenus. Quelle valeur résultante obtient-il ?
d) Il "monte" toutes les notes de 2 points ; quelle est alors la valeur de la moyenne ? Il
multiplie chaque note par 2 ; combien vaut alors la moyenne ?
De quelles propriétés ces résultats témoignent-ils ?
e) Quelle est l'étendue de cette distribution ?
Quelle est la valeur de l'intervalle interquartile ?
Quelle est la variance de cette série ? son écart-type ?
f) En reprenant les deux cas déjà étudiés, que devient l'écart-type :
. quand on "monte" chaque note de 2 points ?
. quand on multiplie chaque note par 2 ?
g) Quelle est la valeur du 5° décile de cette distribution ?
Quel est le nombre d'éléments supérieurs au 2° décile ? inférieurs au 6° décile ?

2
Combien y a-t-il d'unités entre le 3° et le 8° décile ?
Exercice 8: Aux Jeux Olympiques, les matchs de hand-ball (hommes) ont été disputés en deux
tournois (groupe A et groupe B) suivis d'une finale (F). Les résultats sont portés dans le tableau ci-
dessous.
RFA Yougo URSS Danemark Japon Canada
RFA * 18-17 16-18 18-14 19-16 26-11
Yougo * 20-19 25-17 26-22 22-18
URSS * 24-16 26-16 25-9
Danemark * 21-17 24-18
Japon * 25-19
Canada *
Groupe A
Roumanie Pologne Théco. Hongrie USA
Roumanie * 17-15 19-19 23-18 32-19
Pologne * 21-18 18-16 26-20
Théco. * 20-22 28-20
Hongrie * 36-21
USA *
Groupe B
URSS-Roumanie 19-15
RFA - Pologne 18-21
Yougoslavie - Hongrie 21-19
Danemark - Tchécoslovaquie 21-25
Japon - USA 27-20
Finale (F)
On regroupe tous ces résultats dans un seul ensemble de données. On considère la variable x :
"nombre total de buts marqués par match".
a) Regrouper toutes les données dans des classes d'intervalles 3 et choisir 33 comme centre d'une
classe.
b) Etablir le tableau complet des effectifs de classe. Dessiner la représentation des fréquences
relatives et le polygone des fréquences cumulées.
c) Calculer la médiane et le 3ème décile. Quel est la valeur de l'intervalle interquartile ?
Quel est le mode de la distribution ?
Calculer la moyenne et l'écart-type de la distribution de la variable x.
d) On considère successivement les 3 cas suivants :
. à chaque match, 3 buts supplémentaires ont été marqués : y = x + 3
. à chaque match, le double de buts a été marqué : n = 2x
. on a : t = 3x + 1
Pour chacune de ces trois distributions, indiquer la valeur de la moyenne et de l'écart-type.
e) Donner le classement final (des trois premières équipes seulement). Dans chaque tournoi

3
(A et B), quel est le goal-average de chacune de ces trois équipes ? (Par goal-average d'une équipe,
on entend la différence entre le nombre de buts marqués par cette équipe et le nombre de buts encaissés).
Exercice 9 : On veut tester chez des patients greffés cardiaques l’efficacité de deux types
d’entraînement effectués sur 6 semaines: le programme à charge continue (CC) et celui par intervalles
(IT).
Dix sujets sains et 10 sujets greffés cardiaques ont été recrutés. Dans chacun des groupes, cinq
personnes ont suivi 6 semaines de CC et cinq personnes ont suivi un IT.
Avant le début du programme d’entraînement, chaque sujet a complété une épreuve d’effort à charge
constante. La fréquence cardiaque maximale atteinte à l’issue de ce test a été notée (FC1). Ce test a
été répété après les 6 semaines d’entraînement à même charge de travail. La FC atteinte à la fin de
l’épreuve a été notée (FC2). Les résultats de l’étude figurent dans le tableau 1 ci-dessous :
1- Identifiez les variables dépendantes et indépendantes
2- Imaginez une variable parasite
3- Identifiez le groupe expérimental, contrôle et placebo
4- Les groupes sont-ils appariés ou indépendants ?
5- Est-ce une étude transversale ou longitudinale ?
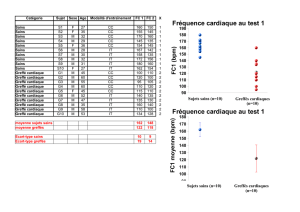
6- Comparez la FC1 chez les sujets sains et les greffés cardiaques. Comparez ces données en
choisissant un graphique approprié. Qu’observez-vous ?
7- Au sein des deux groupes confondus, y a-t-il un lien de causalité entre l’âge et la FC1 ?
Représentez graphiquement la corrélation.
8- Quelles sont les interactions possiblement observées entre :
- la catégorie
- la modalité d’entraînement (CC ou IT)
- FC1
- FC2
Choisissez et construisez un graphique mettant en évidence ces interactions.
Quelles sont les conclusions de cette étude ?

4
Tableau 1 : Résultats de l’étude
9- En utilisant les données des sujets greffés cardiaques, calculez les effectifs des classes
suivantes :
Tableau 2 : Effectifs
Sujets sains Greffés
cardiaques
[80-100[ ? ?
[100-120[ ? ?
[120-140[ ? ?
[140-160[ ? ?
[160-180[ ? ?
[180-200[ ? ?
Faîtes un histogramme sous forme de polygone statistique à partir des données des sujets greffés
cardiaques.
10- Tous sujets confondus, calculer le mode de la distribution précédente. Que constatez-vous ?
Catégorie Sujet Sexe Age Modalité d'entraînement FC 1 FC 2
Sains S1 F 27 CC 160 150
Sains S2 F 35 CC 155 145
Sains S3 M 32 CC 170 160
Sains S4 M 29 CC 145 135
Sains S5 F 36 CC 154 145
Sains S6 M 28 IT 167 142
Sains S7 M 30 IT 158 135
Sains S8 M 32 IT 172 156
Sains S9 M 31 IT 180 160
Sains S10 F 27 IT 162 154
Greffé cardiaque G1 M 45 CC 100 110
Greffé cardiaque G2 M 60 CC 120 100
Greffé cardiaque G3 M 55 CC 95 105
Greffé cardiaque G4 M 60 CC 110 120
Greffé cardiaque G5 F 45 CC 115 110
Greffé cardiaque G6 M 52 IT 140 135
Greffé cardiaque G7 M 47 IT 135 130
Greffé cardiaque G8 M 35 IT 160 140
Greffé cardiaque G9 M 58 IT 110 100
Greffé cardiaque G10 M 53 IT 134 128

5
11- Calculez la moyenne, la médiane et le mode de la FC avant et après entraînement dans la
population entière puis dans les 2 groupes.
Exercice 10 : Inventez une situation nécessitant une comparaison statistique que vous pourriez
rencontrer dans votre futur emploi. Faîtes les mesures descriptives et les graphiques nécessaires pour
apporter vos conclusions.