L`Imagerie par Résonance Magnétique

L’Imagerie par Résonance Magnétique
Bruno Quesson
[email protected]

Résonance Magnétique Nucléaire (RMN)
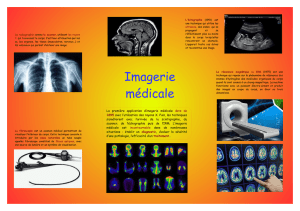
zPrincipe : utiliser les propriétés d’aimantation des noyaux des atomes d’Hydrogène pour imager les
tissus biologiques
zMise en œuvre : utilisation d’un aimant statique puissant B0
–Création d’un état d’équilibre magnétique -> apparition d’une aimantation macroscopique notée « M0 »
zPerturbation de cet état d’équilibre à l’aide d’un second champ magnétique B1, oscillant à la
pulsation ω0 = γB0 , γest le rapport gyromagnétique
(constante physique liée au noyau, ex γ(1H) = 267.106rad/Tesla)
zL’aimantation M0 bascule autour de B1 d’un angle α, qui dépend de l’amplitude de B1
zAussitôt après l’arrêt de la perturbation B1, on observe un retour progressif à l’état d’équilibre
magnétique initial (alignement avec B0)
–L’aimantation revient s’aligner avec B0 en décrivant une mouvement spiralé autour de l’axe parallèle à
B0, avec la fréquence ω0. C’est un « mouvement de précession libre »
–Ce retour est décrit par 2 temps caractéristiques : T1 et T2
zT1 est le temps de relaxation longitudinal (retour vers l’alignement avec B0)
zT2 est le temps de relaxation transverse (disparition du signal dans le plan transverse)
–Les équations de Bloch décrivent l’évolution du mouvement dans le plan transverse et suivant l’axe
longitudinal
–Seule la composante de l’aimantation transverse donne un signal détectable à l’aide d’une antenne
radiofréquence.

Formalisme mathématique
zL’axe parallèle à B0 est noté l’axe « z » ou axe longitudinal
–L’évolution de l’aimantation Mz est décrit par une fonction exponentielle du type
zMz(t) = M0 – [ M0 – Mz(0)].exp(-t/T1)
–Exemples :
zaprès une impulsion B1 d’angle 90°, Mz(0)=0, ce qui conduit à : Mz(t) = M0 [1-exp(-t/T1)]
zaprès une impulsion B1 d’angle 180°, Mz(0)=-M0, ce qui conduit à : Mz(t) = M0 [1-2exp(-t/T1)]
zL’aimantation dans le plan transverse décrit un mouvement de spirale amortie
zCette aimantation est décrite par le formalisme des nombres complexes
–L’axe horizontal dans le plan transverse est l’axe des réels
–L’axe vertical du plan transverse est l’axe des imaginaires
–Ceci conduit à :
zMT(t) = MT(0).exp(-t/T2).exp(iω0t)
–Si à t=0, toute l’aimantation M0 est disponible, Mt(0) = M0
–Si on ne laisse pas à l’aimantation le temps de revenir à son état d’équilibre avant de la
perturber à nouveau (par l’application d’une impulsion B1), MT(0) < M0 et on crée une
saturation partielle du signal (ou totale si t <<<T1)

Quelques remarques
zL’antenne qui recueille le signal capte l’ensemble des petits signaux élémentaires de
tous les protons qui reviennent vers leur état d’équilibre magnétique
zCe signal varie au cours du temps et son amplitude est donnée par l’équation MT(t).
zSi dans l’échantillon placé dans l’aimant, il existe plusieurs types de molécules
contenant des protons (exemple eau et lipides) qui oscillent à des fréquences légèrement
différentes (de quelques hertz par rapport à 64 MHz pour un champ magnétique de
1.5T), alors il est possible de les distinguer en effectuant une opération mathématique
sur le signal observé. Cette opération est une transformation de Fourier, qui substitue à
l’axe des temps un axe de fréquences.
zLes signaux de l’eau et des lipides pourront ainsi être distingués facilement. Il sera
notamment possible de quantifier le contenu respectif d’eau et de lipides en mesurant les
surfaces respectives des pics individuels.
zCependant, avec cette technique il est impossible de distinguer 2 molécules d’eau
provenant de deux régions différentes, puisque celles-ci oscillent à la même fréquence

Obtention d’une image : Imagerie de Résonance Magnétique
zComme les molécules de même nature (ex eau) oscillent à la même fréquence
(ν0=ω0/2π), l’idée est de les forcer à osciller à des fréquences différentes (et
déterminées par l’expérimentateur) en fonction de leur position
zCeci est réalisé à l’aide de Gradients de champ magnétiques, par exemple sur les 3 axes
du repère cartésien lié à B0 : Gx, Gy et Gz
zDans ces conditions, ω0 dépend de x (y ou z) et le signal recueilli s’exprime (à une
dimension) par une transformée de Fourier spatiale
zLe signal est mesuré dans le plan de Fourier, puis l’image est obtenue en appliquant une
transformation de Fourier inverse
zGrâce à l’utilisation de gradients de champs magnétiques, il est possible de :
–Sélectionner une tranche de l’objet
–Créer n’importe quelle trajectoire dans le plan de Fourier (cartésienne, spirale, radiale,
etc.), puisque la position dans ce plan est donnée par la surface (mathématiquement une
intégrale) du gradient d’amplitude G appliqué pendant un temps T.
–De faire de l’imagerie 3D, en réalisant un codage avec des gradients dans 3 directions
orthogonales de l’espace. Bien sûr, cela nécessite une transformation de Fourier à 3
dimensions