Nom

Ministère de l’enseignement supérieur et de la recherche scientifique
Université M’hamed Bougara-Boumerdès – Faculté des Sciences LMD/ST 2011/2012
Nom:…………………….Prénom:……………………Matricule:…………….Section:………….Groupe: …..Note:……/15
Contrôle Continu N°1 (amphy 09) UEF Matière Physique 01
Mercredi 01 Février 2012 Durée : 30 mn Sujet 01
Exercice. 1: (5 points)
1°) Soient deux vecteurs :
14 4 2U i j k  
, et
22U i y j k   
.
Calculer le produit scalaire :
12
()UU
, puis déterminer la valeur de y pour que les vecteurs
1
U
et
2
U
soient colinéaires (c’est-à-dire parallèles ou bien confondues). (1.25 Points)
Réponse
Calcul du produit scalaire par la méthode analytique on a :
12
( ) (4 4 2 ) ( 2 ) (4)( 2) ( )( 4) ( 2)( 1) 4 10U U i j k i y j k y y                 
La valeur de y pour que les vecteurs
1
U
et
2
U
soient colinéaires
12
( ) 0UU  
; (0.25 Point)
12
( ) (4 4 2 ) ( 2 ) 4 4 2 (2 4) ( 4 4) (4 8)
21
i j k
U U i j k i y j k y i j y k
y
;
12 2 4 0 2
( ) 0 4 8 0 2
yy
UU yy
;
En résumé on a :
12
( ) 2(2 5)U U y   
(0.5 Point) et
2y
(0.5 Point)
2°) La vitesse de propagation V d’une onde sur une corde dépend de la tension T (T est une force)
et la masse linéique  (masse par unité de longueur). En utilisant l’analyse dimensionnelle:
a)Trouver la formule de la vitesse V. (2.25 Points)
Réponse
La vitesse V peut être mise sous la forme suivante avec k=1, en utilisant l’analyse dimensionnelle
on aboutit :
V kT
,
V k T
,
12
(LT k M L T M L
, (0.75 Point)
avec k=1 : on fait l’identification :
:1 11
:0 ,
22
: 1 2
L
M
T
(0.5 Point)
T
V
(1 Point)
b) On mesure la tension T=16N à 0.5N près, et la masse linéique =4kg/m à 2% près, déterminer
l’incertitude relative sur la vitesse V. (1.50 Points)
Réponse
1 1 1 1 0.5 2
(0 0.0256.5 Poi
2 2 2 2 2 16 1
nt ) 2 00
T dV dT d V T
LnV Ln V T V T
2.56%
V
V
(1 Point)

Ministère de l’enseignement supérieur et de la recherche scientifique
Université M’hamed Bougara-Boumerdès – Faculté des Sciences LMD/ST 2011/2012
Exercice. 2: (10 points)
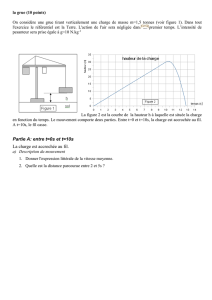
Un mobile M se déplace sur une trajectoire
rectiligne, sa vitesse v(t) est représentée sur la
figure ci-contre, à t=0s, x0 = 0 et v0 = +1.5m/s.
1°) Donner les phases en précisant la nature du
mouvement.
2°) Tracer les diagrammes de a(t) et x(t).
3°) Calculer la distance parcourue sur [0,6s].
Réponse
Variante A
v(t)
t(s)
012 3 4 5 6 7 8 9 10
1.5
1
0.5
-1.5
-1
0.5
m/s
Il existe quatre phases : (1 Pt)
2
[0,3s] v(t) = -0.5t +1.5 (m/s) ( ) 0.5( / )
dv
a t m s
dt
(0.5 Pt); Mouvement décéléré (
.0av
)(0.25 Pt)
2
[3,6s] v(t) = -0.5t +1.5 (m/s) ( ) 0.5( / )a t m s  
(0.5 Pt) Mouvement accéléré (
.0av
)(0.25 Point)
2
[6,9s] v(t) = -1.5 (m/s) ( ) 0( / )a t m s
(0.5 Pt) Mouvement uniforme (vitesse constante) (0.25 Pt)
2
[9,10s] v(t) = 0 (m/s) ( ) 0( / )a t m s
(0.5 Pt) Arrêt (0.25 Point)
Les équations de x(t) sont pour chaque phase :
0
2
00
[0,6s] v(t) = -0.5t +1.5 (m/s) ( ) , ( .5 1.5) ( ) 1.5
4
xt
xt
dx t
v t dx t dt x t t
dt 
; (1.5 Pt)
06
[6,9s] v(t) = -1.5 (m/s) ( ) 1.5 ( ) 1.5 9( )
xt
t
x t dt x t t m
(1 Point)
4.5 6
[9,10s] v(t) = 0 (m/s) ( ) 0 0 ( ) 4.5( )
xt
t
x t dt x t m
(0.5 Point)
2/Le tracé des graphes
(0.5 Point) (1.5 Points)
3°) La distance parcourue par le mobile M sur l’intervalle [0,6s]:
Elle se calcul aisément par l’aire sous la courbe de la vitesse v(t),
2
11
1.5 3 1.5 3 4.5
22
Aire m      
0,6 4.50 s
dm
(1 Point)

Ministère de l’enseignement supérieur et de la recherche scientifique
Université M’hamed Bougara-Boumerdès – Faculté des Sciences LMD/ST 2011/2012
Nom:…………………….Prénom:……………………Matricule:…………….Section:………….Groupe: …..Note:……/15
Contrôle Continu N°1 (amphy 09) UEF Matière Physique 01
Mercredi 01 Février 2012 Durée : 30 mn Sujet 02
Exercice. 1: (5 points)
1°) Soient deux vecteurs :
13 4 2U i j k  
,
22 12U i y j k   
.
Calculer le produit vectoriel :
12
()UU
, puis déterminer la valeur de y pour que les vecteurs
1
U
et
2
U
soient perpendiculaires. (1.25 Points)
Réponse
12
( ) (3 4 2 ) ( 2 12 ) 3 4 2 ( 48 2 ) ( 4 36) (3 8)
2 12
i j k
U U i j k i y j k y i j y k
y
;
La valeur de y pour que les vecteurs
1
U
et
2
U
soient perpendiculaires
12
( ) 0UU  
; (0.25 Pt)
12
( ) (3 4 2 ) ( 2 12 ) (3)( 2) ( )( 4) (2)(12) 4 18U U i j k i y j k y y               
En résumé on a :
12
( ) 2( 24) 40 (3 8)U U y i j y k      
(0.5 Pt) et
9
2
y
(0.5 Pt)
2°) La Tension (T est une force) appliquée sur une corde dépend de la vitesse de la propagation V
de l’onde et la masse linéique  (masse par unité de longueur).En utilisant l’analyse dimensionnelle:
a)Trouver la formule de la tension T. (2.25 Points)
Réponse
La tension T peut être mise sous la forme suivante avec k=1, en utilisant l’analyse dimensionnelle
on aboutit à :
T kV
,
T k V
,
2
MLT k L T M L k M L T
,(0.75 Pt)
avec k=1 : on fait l’identification :
:1
:1 2 , 1
:2
L
M
T
(0.5 Point)
2
TV
(1 Point)
b) On mesure la vitesse de l’onde v=2m/s à 1.81%, la masse linéique =40g/cm à 0.8g/cm près,
déterminer l’incertitude relative sur la tension T. (1.50 Points)
Réponse :
2(0. 1.81 0.8
2 2 2 0.0562
100 40
5 Pt)
dT dV d T V
LnT LnV T V T V
5.62%
T
T
(1 Point)

Ministère de l’enseignement supérieur et de la recherche scientifique
Université M’hamed Bougara-Boumerdès – Faculté des Sciences LMD/ST 2011/2012
Exercice. 2: (10 points)
Un mobile M se déplace sur une trajectoire
rectiligne, sa vitesse v(t) est représentée sur la
figure ci-contre, à t=0s, x0=0 et v0=-1.5m/s.
1°) Donner les phases en précisant la nature du
mouvement.
2°) Tracer les diagrammes de a(t) et x(t).
3°) Calculer la distance parcourue sur [3,10s].
Réponse
v(t)
t(s)
012 3 4 5 6 7 8 9 10
1.5
1
0.5
-1.5
-1
0.5
Variante B
m/s
Il existe quatre phases : (1 Pt)
2
[0,3s] v(t) = 0.5t -1.5 (m/s) ( ) 0.5( / )
dv
a t m s
dt
(0.5 Pt); Mouvement décéléré (
.0av
)(0.25 Pt)
2
[3,6s] v(t) = 0.5t -1.5 (m/s) ( ) 0.5( / )a t m s
(0.5 Pt); Mouvement accéléré (
.0av
)(0.25 Pt)
2
[6,9s] v(t) = 1.5 (m/s) ( ) 0( / )a t m s
(0.5 Pt); Mouvement uniforme (vitesse constante) (0.25 Pt)
2
[9,10s] v(t) = 0(m/s) ( ) 0( / )a t m s
(0.5 Pt); Arrêt (0.25 Pt)
Les équations de x(t) sont pour chaque phase :
0
2
00
[0,6s] v(t) = 0.5t -1.5 (m/s) ( ) , (.5 1.5) ( ) 1.5
4
xt
xt
dx t
v t dx t dt x t t
dt 
; (1.5 Pt)
06
[6,9s] v(t) = 1.5 (m/s) ( ) 1.5 ( ) 1.5 9( )
xt
t
x t dt x t t m
; (1 Pt)
4.5 9
[9,10s] v(t) = 0 (m/s) ( ) 0 0 ( ) 4.5( )
xt
t
x t dt x t m
; (0.5 Pt)
2/Le tracé des graphes
(0.5 Point) (1.5 Points)
3°) Distance parcourue par le mobile M sur l’intervalle du temps [3,10s] :
Elle se calcul aisément par l’aire sous la courbe de la vitesse v(t),
2
11.5 (6 3) 1.5 (9 6) 0 6.75
2
Aire m        
3,10 6.75 s
dm
(1 Point)

Ministère de l’enseignement supérieur et de la recherche scientifique
Université M’hamed Bougara-Boumerdès – Faculté des Sciences LMD/ST 2011/2012
Nom:…………………….Prénom:……………………Matricule:…………….Section:………….Groupe: …..Note:……/15
Contrôle Continu N°1 (amphy 04) UEF Matière Physique 01
Mercredi 01 Février 2012 Durée : 30 mn Sujet 03
Exercice. 1: (5 points)
1°) Soient deux vecteurs :
12 3 2U i j k  
,
23 10U i y j k   
.
Calculer le produit vectoriel :
12
()UU
, puis déterminer la valeur de y pour que les vecteurs
1
U
et
2
U
soient perpendiculaires. (1.25 Points)
Réponse
Calcul du produit vectoriel
12
()UU
est :
12
( ) (2 3 2 ) ( 3 10 ) 2 3 2 ( 30 2 ) ( 6 20) (2 9)
3 10
i j k
U U i j k i y j k y i j y k
y
;
La valeur de y pour que les vecteurs
1
U
et
2
U
soient perpendiculaires
12
( ) 0UU  
; (0.25 Pt)
12
( ) (2 3 2 ) ( 3 10 ) ( 3)(2) ( )( 3) (2)(10) 3 14U U i j k i y j k y y               
En résumé on a :
12
( ) 2( 15) 26 (2 9)U U y i j y k      
(0.5 Point) et
14
3
y
(0.5 Point)
2°) Un mobile est animé d’une accélération a à partir du repos, qui dépend de la distance
parcourue d et de sa vitesse V, la constante de proportionnalité étant égale à
0.5k
. En
utilisant l’analyse dimensionnelle :
a)Trouver la formule de l’accélération a. (2.25 Points)
Réponse
L’accélération a peut être mise sous la forme suivante, en utilisant l’analyse dimensionnelle:
a kV d
,
a k V d
,
2
LT k L T L k L T
, (0.75 Point)
avec k=.5 : on fait l’identification :
:1 2 , 1
:2
L
T
(0.5 Point)
2
2
V
ad
(1 Point)
b) On mesure la distance d=10m à 5% près, la vitesse V=2m/s, à 0.5m/s près, déterminer
l’incertitude relative sur l’accélération a. (1.50 Points)
Réponse
21
2
22
V da dV
Lna Ln Ln
d a V
    ( ) 0.5 5 2 2 0.5(0.5 Point) 5
2 100
d d a V d
d a V d
55%
a
a
(1 Point)