1 - Technologue pro

1
Convertisseurs Analogique/Numérique
1. INTRODUCTION
De nos jours on veut minimiser le coût de nos travaux et maximiser nos gains
dans tout les domaine prenant par exemple l’électronique on veut réaliser des
composantes électronique capable de faire n’importe quelle application avec un
minimum de matière c’est la ou les chercheurs ont trouvé la solution la numérisation
donc on peut dire que le monde entier est « analogique »ou traité par des êtres
humains. La conversion Analogique Numérique permet le traitement par des
machines de données digitales. Les techniques actuelles font de plus en plus appel
au traitement numérique, très performant. Le domaine des télécommunications est
sans doute celui dans lequel l’application des techniques numériques est la
plus développée (numérisation de la voix pour la téléphonie, généralisation du FAX et
du courrier électronique, enregistrement numérique des disques…). Sans oublier le
domaine musical qui utilise grandement les convertisseurs dans la transmission des
signaux audio. La numérisation permet d’obtenir la solution des applications complexes
avec l’optimisation du coût, du gain et la dimension du produit comme on a pu voire les
petite dimension que peut occuper un téléphone GSM ou un ordinateur portable ect,
mais pour le moment on n’a pas réussie à tout numériser comme par exemple les
boites d’alimentions de toutes sortes de machines (ordinateur, télévisions…).
L'électronique est en effet divisée en deux domaines distincts :
- le domaine analogique , où les variables peuvent prendre une infinité de valeurs
différentes ; les signaux varient continûment. Tous les signaux issus des capteurs
sont analogiques, et traduisent des phénomènes physiques qui varient continûment.
- le domaine numérique , où les variables prennent uniquement deux états, un état
haut et un état bas.
Beaucoup de signaux était avant traités de façon analogiques et le sont aujourd'hui par
programmation de microprocesseurs.
Les Convertisseurs Analogique Numérique (CAN, ADC en anglais, pour analog to
digital converter), qui vont transformer les tensions analogiques en signaux logiques
prêtes à être traités par microprocesseur (numérisation des signaux).
Les applications d’un convertisseur analogique numérique :
Les applications dans lesquelles des données analogiques doivent être numérisées et
transférées dans une mémoire d’ordinateur sont nombreuses. Le processus de
saisie par l’ordinateur des données analogiques numérisées s’appelle l’acquisition de
données. Selon l’application, l’ordinateur peut manipuler les données de différentes
façons. Quand on utilise un ordinateur pour mémoriser une donnée analogique
(c’est le cas d’un oscilloscope numérique), ce dernier stocke les données puis
les transfère à un CNA à un moment ultérieur pour qu’il reproduise les données
analogiques. On trouve donc des CAN dans les multimètres numérique, les systèmes
d'acquisition, l’élaboration de la matrice d’un disque compact...

2
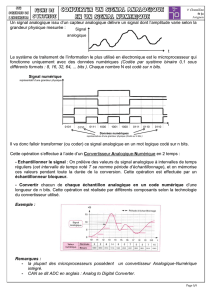
Les étapes de la conversion analogique numérique (numérisation)
La conversion d’un signal analogique en un signal numérique se fait en 3 étapes
Fig1 :les étapes de la numérisation
2. Les étapes d’une conversion d’un signal analogique en numérique :
Un convertisseur analogique numérique est chargé de transformer une variation
continue de tension en une série de valeurs mathématiques (sans énergie) codées
La conversion d’un signal analogique en un signal numérique se fait en 3 étapes
l’échantillonnage, La quantification puis Le codage
Echantillonnage :
Notons par x
a
( t ) le signal analogique de d é part. La constitution du signal é chantillonn é
x
e
( t ) est obtenu par multiplication de ce signal analogique par un train d ’ impulsions de
Dirac d ’ amplitude unit é et é qui-éspacé es de
e
T
C e train est not é p ( t ) et il est d éfi ni par
nnTettp )()(
Le signal é chantillonn é corr espond donc à
n
aae nTttxtptxtx )()()()()(
D’après la pr opri é t é f ( t ) δ ( t ) = f (0) δ ( t ) , o n a encor e
naa nTtntxtx )()()(
Fig3 : Signal de depart Fig4 : Train d’impulsions de Dirac

3
Fig5 : Le signal échantillonné
Cette figure nous montre l’ Op é ration associ ée à l ’ obtention d ’ un signal é chantillonn é : multipli cation
par un train d ’ impulsions
Théorème de l’échantillonnage : Théorème de Shannon :
p(t) est périodique et peut donc être développé en série de Fourier. Le résultat est
k
Tktj
e
T
tp /2
1
)(
Par application du théorème de modulation, le spectre de p(t) est donné par
kTkw
T
wp )/2(
2
)(
)(txe
etant le signal échantillonné est donné par le produit de convolution avec xa(t) avec p(t)
)()()( tptxtx ae 
La convolution d’un signal avec un train d’impulsions se fait en reproduisant le signal au droit de
chacune des impulsions. Le spectre du signal échantillonné est donc donné par
kae tktx
T
tx )/(
1
)(

4
On voit donc que l’effet de l’échantillonnage est de périodiser le spectre du signal analogique de
départ. Cette périodisation se fait à un rythme 1/T en fréquence.
Le théorème de Shannon s’intitule en :
Si f la fréquence du signal et
e
f
la fréquence de l’échantillonnage pour obtenir un signal échantillonné
sans chevauchement il faut que
e
ff 2
 Quantification:
Numériser un signal analogique implique qu'on doit le coder à l'aide d'un nombre fini de
symboles; c'est l'opération de quantification. Quantifier un signal revient à approximer sa
valeur instantanée par la valeur discrète la plus proche. On commet donc une erreur.
Quantification uniforme : est la plus utilisée de pas constant :
-quantification uniforme par arrondi
- quantification uniforme par troncature
Quantification avec compression de donnés a pas variable
Pas de quantification constant Pas de quantification variable
Rapport signal-sur-bruit de quantification
Lorsque l'on effectue une approximation du signal original, on commet forcément une erreur
relativement à la représentation originale du signal. Cette erreur est appelée erreur de
quantification.
A cette erreur de quantification est associée, lors de l'écoute, une perturbation, que l'on
appelle bruit de quantification.
L'effet du bruit de quantification relativement au signal original constitue ce que l'on nomme
le rapport signal-sur-bruit de quantification.

5
Quantification lineaire
En pratique, on n'échantillonne pas un signal pour le reconstruire juste après.
L'échantillonnage est utilisé pour prélever le signal à des instants multiples de Te et ensuite
convertir les échantillons sous forme d'un code binaire (8, 12, 16 bits, ...). En général, juste
derrière l'échantillonneur on place un bloqueur pour maintenir le signal constant à l'entrée du
convertisseur analogique-numérique (CAN) pendant la durée de conversion, nombre de CAN
fonctionnent cependant sans bloqueur. Le schéma de principe d'un échantillonneur-bloqueur
(Sample and Hold) est donné à la Fig. 6, (exemple de circuit : AD585 de Analog Devices,
voir annexe I). En téléphonie ou télévision numérique le signal codé module une porteuse en
phase, à la réception un démodulateur transforme de nouveau le signal reçu en code et un
convertisseur-numérique analogique permet de restituer un signal analogique
Fig6 :schéma du principe d’un échantionneur bloqueur
C'est l'opération qui consiste à associer une valeur analogique à la plus petite variation
mesurable entre deux valeurs codées distinctes en sortie. Cette valeur est appelée
quantum.
Code non signé