Vocabulaire mathématique, notation et symboles - FR

ESIEE Paris – E3FI Carmelo Guarneri
Vocabulaire mathématique, notation et symboles
I. Quelques notations et symboles
Symbole Définition
∀
Quelque soit
∃
Il existe
⇒
implique
x∈E
x appartient à E
x∉E
x n'appartient pas à E
∅
Ensemble vide
II. Un peu de logique : contraposée et réciproque d'une implication.
En mathématique l'implication correspond à la phrase « si P1 alors P2 » qui relie deux propositions
P1 et P2.
On écrit cette phrase « P1
⇒
P2 » et elle peut être traduite par « non P1 ou P2 » .
Exemple :
L'implication suivante est vraie :
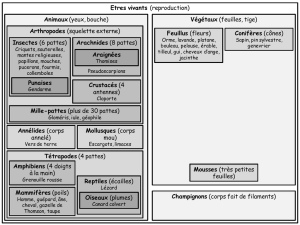
Si un animal est un homme alors il peut parler.
L'implication suivante est fausse :
Si un animal a deux pattes alors c'est un hommeSi un animal a deux pattes alors c'est un homme
a. Contraposée
La contraposée de « P1
⇒
P2 » est « non P2
⇒
non P1 » .
La contraposée d'une proposition vraie est toujours vraie.
La contraposée d'une proposition fausse est toujours fausse.
Exemple :
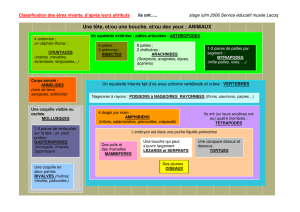
Si un animal est un homme alors il marche sur deux pattes.
Si un animal ne marche pas sur deux pattes alors ce n'est pas un homme.
b. Réciproque
La réciproque de « P1
⇒
P2 » est « P2
⇒
P1 » .
La réciproque d'une proposition vraie n'est pas forcement vraie.
Exemple :
Si un animal est un homme alors il marche sur deux pattes.
Si un animal marche sur deux pattes alors c'est un homme.
4

ESIEE Paris – E3FI Carmelo Guarneri
III. Ensembles, réunions, intersections.
-Un ensemble est une collection d'objets tous différents. Ses éléments peuvent être écrit dans l'ordre
que l'on veut. Un ensemble peut être fini ou infini.
Exemple :
La collection des nombres 7, 3, 5 et 2 est un ensemble fini, on le note
{7,3, 5,2}
et
{7,3, 5,2}
=
{3,5, 2,7}
.
L'ensemble
{1,... , n}
de tout les nombres entier entre 1 et n est aussi noté
⟦1, n⟧
.
La collection des nombres entiers est un ensemble infini, on le note
ℕ
.
La réunion de deux ensembles E et F est l'ensemble qui contient tout les éléments de E et de F.
On la note
E∪F
.
Exemple :
E={7,3,5}
,
F={2,7,10, 3}
,
E∪F={2,7,10, 3,5}
L'intersection de deux ensembles E et F est l'ensemble qui contient tout les éléments qui sont à la
fois dans E et dans F. On la note
E∩F
.
Exemple :
E={7,3,5}
,
F={2,7,10, 3}
,
E∩F={7, 3}
IV. Familles, Sommation sur une famille, signe ∑ .
-Une famille d'éléments d'un ensemble est une liste d'objets ordonnée. Un objet de cette liste est
appelé un terme. Deux termes d'une liste peuvent être identiques et sont différenciés par leur ordre.
Exemple :
La famille
(7,3,5, 2,7, 2)
est une liste des nombres, le troisième terme de cette liste est le nombre
5, les quatrièmes et sixièmes termes de cette liste sont égaux.
La famille
(3,7,5, 2,7, 2)
est différente de la famille précédente bien que constituée des mêmes
nombres car ses termes sont dans un ordre différent.
Une famille peut avoir un nombre de termes infini.
L'expression
∑
i=1
p
xi
est la somme de tout les éléments de la la famille
(x1, ... , x p)
.
Dans le cas d'une famille finie, l'ordre de sommation n'as pas d'importance, mais si la famille est
infinie alors on doit sommer les termes dans l'ordre où ils se présentent.
V. Produit de deux ensembles
L'ensemble ExF={(x,y) où
x∈E
et
y∈F
} est l'ensemble des familles a deux termes dont le
premier terme est dans E et le deuxième dans F.
On peut généraliser ce produit à n ensembles
(E1, ... , E2)
on a alors :
E1×...×En
={
(x1, ... , xn)
où
∀xi∈⟦1, n⟧
xi∈Ei
}.
Exemples :
-
ℝ2=ℝ×ℝ
,
ℝ3=ℝ×ℝ×ℝ
,
ℝ4=ℝ×ℝ×ℝ×ℝ
,
ℝn
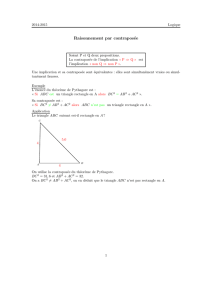
- E={ 4, 9 , 10}, F={9, 10, 11}
ExF={(4,9), (4,10), (4,11), (9,9), (9,10), (9,11), (10,9), (10,10),(10,11)}
5

ESIEE Paris – E3FI Carmelo Guarneri
VI. Relation d'équivalence.
En mathématique la relation d'équivalence se définit sur un ensemble et sert dans tous les domaines,
aussi bien pour l'analyse que pour l'algèbre.
En construisant une relation d'équivalence on crée une partition de l'ensemble qui permet de classer
les éléments d'un ensemble en classe d'équivalences qui vont servir à créer un nouvel ensemble plus
facile à manipuler.
Définition:
Soit E un ensemble, une relation d'équivalence R notée ~ est une relation entre les éléments :
i)
∀x∈E
x
~
x
(réflexivité)
ii)
∀x , y∈E
x
~
y
⇒
y
~
x
(symétrie)
iii)
∀x , y , z ∈E
x
~
y
et
y
~
z
⇒
x
~
z
(transitivité)
6