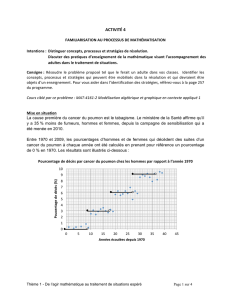
Quand l`industrie mise sur les équations

mathéma
tique
Lemonde
est
Pour Galilée, l’immense livre de la nature
est écrit en termes mathématiques.
Pour l’immense majorité des gens,
ce langage reste opaque :pour eux, les
maths sont souvent un mauvais
souvenir, un instrument de sélection, sur-
tout en France où la fracture entre scien-
ces et lettres paraît parfois irrémédiable.
Et pourtant, «LeMonde»fait le pari que
l’on peut raconter les mathématiques à
tous, et que chacun peut en tirer un
supplément de compréhension de
l’univers dans lequel nous vivons. Ce pari
s’incarne dans une collection d’ouvrages
intitulée «Lemonde est
mathématique», diffusée en kiosques à
compter du 21 mars. On ycroisera des
chiffres et des êtres :pi, le nombre d’or,
Pythagore, Turing ou des perceurs
d’énigmes tel Andrew Wiles. On y
évoluera dans la quatrième dimension,
les arcanes de la finance ou le monde du
cryptage. Pour se lancer dans une pareille
aventure, il faut des passeurs. Cédric
Villani, Médaille Fields 2010 et directeur
de l’Institut Henri-Poincaré, et ses
confrères en vulgarisation de
l’association Images des maths ont
accepté de parrainer cette collection.
Parce que les maths ont toute leur place
dans la culture des honnêtes hommes
et femmes du XXI
e
siècle
Que peuvent bien avoir en commun des
phénomènes naturels aussi différents que
l’agencement des graines d’un tournesol,
l’élégante spirale dessinée des coquillages
et les bras de la Voie lactée ?Quelle règle
géométrique d’une inégalable harmonie se
cache dans l’œuvre des plus grands artistes, de
Vitruve àSalvador Dalí, en passant par Léonard
de Vinci et Le Corbusier ?Aussi incroyable que
cela puisse paraître, la réponse àces deux
questions réside dans un seul nombre :
1,61803398875. Un nombre d’humble
apparence, connu depuis l’Antiquité et dont la
présence remarquée dans les représentations
artistiques et naturelles lui valut le surnom de
«nombre d’or »ou«divine proportion ».
Cahier du «Monde »N˚21204 daté Vendredi 22 mars 2013 -Nepeut être vendu séparément

le monde est mathématique
Entretien
C
édric Villani areçu en 2010 la
médaille Fields, souvent com-
paréeauNobelde mathémati-
ques, qui récompense tous les
quatre ans des chercheurs de
moins de 40 ans. Directeur de
l’Institut Henri-Poincaré (Université Pier-
re et Marie Curie, CNRS) ,ilest depuis deve-
nu l’un des porte-parole majeurs de sa dis-
cipline. Vulgarisateur intarissable, il a
accepté de s’associeractivement àlapubli-
cation par Le Monde d’une collection
d’ouvrages consacrée àcelle-ci, «Lemon-
de est mathématique ». Une initiative qui
rejoint son souci de susciter des vocations
scientifiques, mais aussi de contribuer à
élargir la «culture de l’honnête homme».
Pourquoi l’Institut Henri-Poincaré
(IHP) a-t-il parrainé cette collection?
Les raisons sont multiples mais tour-
nent toutes autour de l’importance de la
vulgarisation scientifique.
D’abord, il faut veiller àsusciter des
vocations en nombre suffisant parmi les
jeunes, àune époque où l’on ne pense pas
naturellementàunecarrièredemathéma-
ticien, ou plus généralement de scientifi-
que, comme àunmétier qui adequoi faire
rêver.C’estpourtant le cas!C’est unmétier
dans lequel subsiste une grande part
d’aventure.Aquelques exceptions près, ce
n’est pas un moyen de faire fortune, mais
c’est un métier qui apporte une excellente
combinaisond’élémentsmatérielsconfor-
tables et de stimulation, de valorisation
intellectuelle. C’est un bon métier, utile à
l’individu et àlasociété.
Il est très importantqu’un nombresuffi-
santdejeunesembrassecettecarrière.Pour
cela, il faut leur apporter un éclair de rêve,
afindelesinciteràselancerdansdesétudes
qui peuvent sembler longues et pénibles,
mais qui le sont moins qu’il n’y paraît, et se
révèlent souvent très gratifiantes.
Ensuite, il faut aussi s’adresser àtous
ceux quineferont pas des sciences leur
métier, mais qui sont curieux de savoir à
quoi ça sert. La vulgarisation remplit la
fonction de rapprocherau niveau intellec-
tuel et sensible les chercheurs et les
autres. C’est important aussi pour des rai-
sons très pratiques:lejour où les gens ne
comprendront plus àquoi servent les
scientifiques, les politiques couperont les
subventionscorrespondanteset la recher-
che s’arrêtera. La communauté scientifi-
que adonc le devoir naturel d’expliquer
ce qu’elle fait aux gens qui la soutiennent.
La mathématique fait-elle partie de la
culture générale?
Oui, il est important et enrichissant
pour tout le monde de comprendre ce qui
aété réalisé avec la mathématique, une
science assez extraordinaire.Comprendre
que ce n’est pas quelque chose d’isolé,
mais quecela concernetout lemonde.Par-
ce que tout le monde utilise les avancées
scientifiques.
En outre, les scientifiques ont aussi
besoin de reconnaissance, de se sen-
tir appréciés, et non d’être dési-
gnés comme des bêtes curieuses
qui font quelque chose de peu
productif, d’incompréhensi-
ble. Dans le passé, certains
des mouvements les
plus durs de contesta-
tion des scientifiques
étaient dus moins àdes
questions matérielles
qu’à des questions de res-
pect, en particulier de la
sphère politique. Cela
me fait penser àcette
citation, attribuée àdeGaulle: «EnFrance,
deschercheurs qui cherchent, on en trouve,
des chercheurs qui trouvent, on en cherche. »
Et voilà comment, pour faire un bon mot,
on aliène une partie fondamentale de la
société avec une pique injuste.
Injuste, car on sait bien que la recher-
che française est de qualité !Onsait bien
aussi qu’il est normal qu’un chercheur
échoue dans ses recherches. La plupart du
temps cela ne marche pas, et c’est normal !
De la même façon qu’on dit que, dans le
domaine industriel, 99 %des brevets sont
non rentables:cequi compte, c’est le 1%
qui reste. Ce n’est pas parce que vous cher-
chez, cherchez, cherchez et ne trouvez
presque jamais que vous êtes un mauvais
chercheur. L’état naturel du chercheur,
c’est d’errer. De temps en temps, il yaun
trucqui marche, il faut le faire fructifier:
«Dans le métier
de mathématicien
subsiste une grande
part d’aventure »
Cédric Villani.
LÉA CRESPI
POUR «LEMONDE »
Entre culture du secret
et arithmétique de la sécurité,
la cryptographie est aussi
vieille que l’écriture !
Présente dès l’Antiquité
dans les hiéroglyphes
égyptiens ou les écrits de
Mésopotamie, on la retrouve
au cœur de la seconde guerre
mondiale dans la machine
Enigma des nazis.
La cryptographie s’illustre
aujourd’hui dans des usages
plus pacifiques :transactions
bancaires, achats sur
Internet…
Divisibles seulement
par 1etpar eux-mêmes,
les nombres premiers sont
un véritable casse-tête.
Mystérieux, indomptables,
ils constituent l’un des plus
grands défis de l’histoire de la
science:Euclide, Fermat, Euler,
Gauss, Riemann, Râmânujan…
La liste est longue de ceux
qui sont tombés dans
leurs filets, succombant
àl’obsession de trouver enfin
la règle présidant àleur
apparition, sans jamais y
parvenir.
Il est le seul mathématicien
dont le nom résonne
familièrement aux oreilles
de tous. Depuis des
générations, les enfants sur
les bancs de l’école récitent son
fameux théorème. Mais qui
était ce Pythagore dont l’aura
atraversé les siècles, nimbée
d’un entrelacs de mystères ?
Deux mille six cents ans après
son invention, son théorème
se glisse dans les applications
les plus communes et les
plus sophistiquées, n’ayant
rien perdu de sa modernité.
II 0123
Vendredi 22 mars 2013

le monde est mathématique
c’est comme cela qu’a fonctionné le pro-
grès humain depuis des millénaires.
De bons livres de vulgarisation existent
déjà. Qu’apporte cette collection ?
C’estvrai.On peut citerleslivresdeMar-
cus du Sautoy, d’Alex Bellos, l’ouvrage de
SimonSinghconsacréauthéorème de Fer-
mat, celui de Donal O’shea sur la conjectu-
re de Poincaré, la bande dessinée Logico-
mix…Pourtant, il manquait encore quel-
que chose, comme une encyclopédie
mathématique. En quarante volumes,
vous pouvez bien développer les idées. Le
fait que ce soit écrit par des auteurs diffé-
rents, avec des angles et des préoccupa-
tionsvariés–historiques,sociaux,esthéti-
ques… –rend cet ensemble plus riche
qu’une encyclopédie avec une grille de
classement unique. Mais attention :cette
collection n’entraîne pas àlaréflexion
logique et àlapratique mathématique
commeseul peut le faire un cours avec
démonstrations et exercices. C’est juste la
cerise sur le gâteau qui raconte combien
cette aventure est passionnante.
Il ne s’agit pas de remplacer les cours de
mathématiques par des exposés de vulga-
risation, ce serait une confusion complè-
te. Mais de compléter les cours systémati-
ques par des exposés d’une autre nature,
montrant le sens, l’histoire. Apetite dose.
Et là vous êtes prêt àvous investir.
Les mathématiques sont perçues com-
me difficiles, comme un instrument de
sélection scolaire :s’agit-il seulement
de clichés ?
Je crois que ce sont des clichés et j’espè-
re que ces livres peuvent ébranler ces
mythes. Quand on fait des conférences de
vulgarisation, presque toujours quel-
qu’un vient vous dire: «Jecroyais que je ne
comprenais rien et finalement je com-
prends,c’est sympathique. Combien je
regrette qu’on ne m’ait pas expliqué cela
quand j’étais élève… »
La mathématique, c’est comme tout :
cela peut se raconter àn’importe quel
degré de complexité. D’ailleurs, l’une des
raisons de mentionner dans mon livre,
Théorèmevivant,lesformulesmathémati-
ques, c’est pour qu’on ait une image, une
idée du degré de complexité que cela peut
atteindre,danslequelmêmenouson n’en-
tre pas quand on discute entre collègues.
Quel que soit le discours, quand on expli-
que, on est toujours en train de trahir, plus
ou moins. Mais, tant que vous avez, com-
me votre interlocuteur, la conscience du
niveau de trahison, celle-ci est justifiée,
pardonnée.
La forme mathématique, l’apprentissa-
ge systématique des concepts, c’est tou-
joursunpeu difficile, douloureux, pour
tout le monde. C’est une gymnastique
cérébrale qui n’est pas naturelle, mais on
est d’autant plus heureux de la faire qu’on
comprend quelles en sont les finalités,
qu’on la replace dans l’histoire des pro-
grès humains, comme objet social, en tant
que création culturelle et artistique.
Que retenez-vous de votre engagement
dans la vulgarisation depuis la médaille
Fields?
C’est une compétence qu’on acquiert et
qu’ondéveloppe pour toucher les gens et
être accessible.L’ensemble du corps scien-
tifiquealongtempsconsidéréavecun peu
de dédain cette activité, mais les temps
changent. C’est aussi quelque chose de
très intense :une sorte de communion
s’établit entre le public et l’orateur. Ce
sont aussi des expériences très majori-
tairement positives. Al’IHP nous
testons de nouvelles formes
pour toucher des publics plus
variés;par exemple, récem-
ment, nous avons lancé des soi-
rées de projection de film suivie de débats
du public avec des mathématiciens. Pour
ladernière,autourdu documentaireCode-
breaker qui raconte la vie d’Alan Turing,
nous avons dû programmer deux séances
et refuser du monde:ilyaunvrai appétit
du public. De telles opérations auront-
elles un impact?C’est difficile àapprécier,
mais je suis persuadé que oui.
D’où vient l’excellence de l’Ecole mathé-
matique française?
Une telle qualité se construit dans la
durée. Elle est d’abord une question de
culture et de transmission. Depuis des siè-
cles, la France est àlapointe dans la recher-
che mathématique mondiale. Le redémar-
rage de cette discipline en Europe remonte
àlaRenaissance. Et dès le XVIIesiècle, en
France,dessavantss’illustrentcommePas-
cal,Fermat,DesarguesouDescartes.Ensui-
te, au moment des Lumières, l’expansion
continue. Cette période n’est en effet pas
seulement un moment humaniste et litté-
raire, elle est également marquée par des
développements spectaculaires en maths.
Le mouvement était lancé et acontinué de
s’enrichird’autresvagues, notamment àla
Révolution. Des institutions comme l’Eco-
le normale supérieure (ENS) ou l’Ecole
polytechnique sont créées pour transmet-
tre les savoir-faire. On retrouvera cette
volonté pendant l’entre-deux-guerres
avec la création du CNRS et du Palais de la
découverte parexemple. Le succès est àla
fois affaire de culture et d’institutions.
Etes-vous inquiet pour l’avenir de cette
Ecole?
Acause de ce contexte favorable, je ne
me fais pas de souci pour la recherche
mathématique en France. Je veux bien
parierqu’il yaura des médailles Fields
françaises en 2014 !
En revanche, on peut être plus inquiet
pour d’autres branches aussi importantes,
moins académiques et plus appliquées,
plus «utilisatrices»des mathématiques,
en liaison avec l’industrie par exemple. Il
est important qu’il yait des personnesavec
une sensibilité scientifique, voire mathé-
matique, dans les entreprises :beaucoup
d’entre elles gagneraient àétoffer leur
département de recherche, ycompris
théorique. Mais encore faut-il qu’elles
ensoientconscientes;etqu’ellesréa-
lisent la compétence française
dans ce domaine !Etpuis,
nous ne formons pas assez
de scientifiques.
Et plus largement, comment se porte
votre discipline?
Elle va bien. Globalement, les effectifs
et le nombre d’articles augmentent. Des
centaines de milliers (!) de théorèmes sont
démontrés chaque année. Il n’y ajamais
eu autant de colloques internationaux
organisés qu’aujourd’hui. Malgré Inter-
net, les gens ont besoin de se rencontrer,
de discuter… Des sujets nouveaux appa-
raissent.Lamathématique est donc loin
d’être quelque chose de figé. Je n’arrive
pas àsuivre l’actualité, ycompris dans les
domaines dont je suis spécialiste !Lepara-
doxe, comme dans les sciences en général,
est que l’on asouvent l’impression de pié-
tiner, mais que si l’on regarde sur le long
terme on réalise àquel point le sujet avan-
ce àune vitesse considérable.
Quelles sont vos «marottes »actuelles ?
Ces temps-ci, j’ai dû mettre des recher-
ches en veilleuse pour me consacrer à
d’autres projets, mais je reviendrai àmes
«marottes»… J’en ai une petite dizaine en
même temps, car il est bon de ne pas se
concentrer sur un seul problème:tantôt
l’unavance,tantôtc’estl’autre.Plusil yade
choses qu’on comprend, plus l’on décou-
vre des questions ouvertes ;chaque fois
qu’on résout un problème, de nouveaux
surgissent!Mon amour de jeunesse reste
la théorie cinétique des gaz et je continue-
raid’y travailler.Maisje m’intéresseaussi à
la géométrie, ou aux liens entre géométrie
et probabilité. Et il yaun problème sur
lequel je rêverais de faire des avancées
même si je ne m’y suis pas encore plongé,
c’est celui des transitions de phase, ces pas-
sages entre deux états, comme celui entre
leliquideetungaz en fonction de la tempé-
rature. On ne sait toujours pas pourquoi la
transition alieu. C’est fascinant.
Le monde est-il réellement mathémati-
que?
On peut débattre pour savoir si le mon-
de est sous-tendu par des règles mathéma-
tiques ou si c’est que nous le voyons de
manièremathématique, c’est-à-dire en
essayant de trouver des règles abstraites
derrière les particularismes concrets qui
nous entourent. On peut penser que le
monde est mathématique dans le sens où
Galilée l’entendait:lemonde est écrit en
caractères mathématiques. Quel que soit
lepointdevue, on nepeutnierquelelanga-
ge mathématique est extrêmement bien
adapté àdécrire le monde qui nous entou-
re. Donc, pour un observateur, c’est com-
me si le monde était mathématique ! p
Propos recueillis par
David Larousserie
et Hervé Morin
Un programme au carré
La collection «Lemonde est
mathématique», lancée par
Le Monde,rédigée par des mathé-
maticiensespagnols, ad’abord
été diffusée par El Pais,avant de
l’être en Belgique et au Royaume-
Uni. Le Monde s’est associé avec
l’éditeur espagnol RBA pour la fai-
re connaître en France. Le pre-
mier tome –consacré au nombre
d’or –est disponible en kiosque
au prix de 3,99¤.
Nouvelle édition Présentée par
Cédric Villani, elle aété réalisée
avec le soutien de l’Institut Henri-
Poincaré (UPMC et CNRS,
www.ihp.fr), qu’il dirige depuis
2009, et en collaboration avec les
animateurs de la revue en ligne
Images des maths,hébergée par
le CNRS
(http ://images.maths.cnrs.fr).
Sur France Inter La collection
«Lemonde est mathématique »
apour partenaire l’émission «La
Tête au carré ». L’ouvrage de la
semaine sera raconté par
Mathieu Vidard àpartir du
21 mars, chaque jeudi, dans son
émission diffusée de 14 heures à
15 heures.
Sur Lemonde.fr Chaque
semaine, des mathématiciens,
dont Cédric Villani, proposeront
un défi mathématique en vidéo.
Leur résolution sera communi-
quée en ligne la semaine suivante
(www.lemonde.fr/defis-mathe-
matique).
La vulgarisation
est quelque chose
de très intense car elle
permet une sorte
de communion entre
le public et l’orateur
Les mathématiques peuvent-elles faire rêver ?
Cédric Villani en est persuadé. Médaille Fields 2010,
il se consacre àlavulgarisation, qu’il juge essentielle
pour faire naître de nouvelles vocations
Il asuffi que les
mathématiciens, emmenés
par le grand Riemann,
démontrent dès le milieu
du XIXesiècle qu’il était
possible de dépasser les trois
dimensions caractérisant
notre expérience du monde
sensible pour captiver
l’imaginaire collectif!
Qui eût cru que ces géométries
nouvelles puissent devenir
une telle source d’inspiration
pour la peinture, la sculpture,
l’architecture et, bien sûr,
le cinéma?
Aquel nombre est dedié
chaque année le 14 mars ?
Aquel nombre un Prix Nobel
de littérature consacra
un poème ?Quel nombre
adonné son nom àunhéros
de jeu vidéo ?
Pi =3,1416... La réponse sonne
comme une évidence.
Mais pourquoi ce chapelet
de chiffres exerce-t-il une telle
fascination?Etquel chemin
parcouru depuis Archimède
qui, l’un des premiers, se lança
dans la recherche d’une
approximation de pi !
Domaine de liberté
par excellence, le jeu avu
apparaître un nouveau groupe
d’influence, celui de
mathématiciens!Menés par
John von Neumann et Emile
Borel, puis John Nash, ils
élaborèrent une discipline
mathématique ayant trait
àlaprise de décision :
la théorie des jeux. Elle permet
de déterminer des stratégies
gagnantes pour aboutir
àdes situations optimales
–enéconomie, lors d’élections,
ou même àlaguerre.
III
0123
Vendredi 22 mars 2013

le monde est mathématique
Comment parcourir les rues
de l’ancienne Königsberg
(l’actuelle enclave de
Kaliningrad) en ne passant
qu’une seule fois sur chacun
des sept ponts qui enjambent la
rivière Pregolia?Sur une carte,
combien faut-il de couleurs
pour que deux pays
limitrophes n’arborent pas
la même ?Comment résoudre
le mystère des «trois carrés
enchâssés», imaginé par Lewis
Carroll?Autant d’énigmes
qui peuvent être résolues grâce
àlathéorie des graphes.
«Enfin, un Eurêka !»
C’est par ce titre du New York
Times que fut célébré,
en 1993, l’un des plus beaux
exploits mathématiques:
la résolution du dernier
théorème de Fermat par le
Britannique Andrew Wiles.
Une aventure scientifique
née plus de trois siècles
auparavant, quand Pierre
de Fermat annonça avoir
trouvé une «merveilleuse
démonstration», sans avoir
eu la place de la noter
dans la marge.
La spongiosité d’un nuage,
les ramifications d’un arbre,
l’irrégularité d’un éclair et
même les dessins ornant la
queue d’un paon royal…
la géométrie fractale décrit
l’ensemble de ces phénomènes
aussi sûrement qu’une sphère
constitue une approximation
de la forme de la Terre.
Géologie, volcanologie,
démographie, économie:
la théorie mathématique
des fractales possède
de nombreuses applications
pratiques. Adécouvrir.
C
hef d’entreprise cherche
mathématicienpourrésou-
dre les problèmes de sa
société.» L’annonce pour-
rait faire sourire, mais,
dans une forme plus orga-
nisée, c’est un peu ce genre d’invitation
quiaconduitquatrereprésentantsd’en-
treprises àl’Ecole nationale supérieure
des mines de Nancy (ENSMN),
débutfévrier, àlarencontre de 25 jeu-
nes docteurs ou doctorants en maths.
Pour cette cinquième Semaine d’étu-
de maths-entreprises (SEME), Arcelor-
Mittal se demandait comment détecter
sur des images des défauts dans son
acier. RTE, le transporteur d’électricité
national, s’interrogeait sur la modélisa-
tion de la production solaire. Le cabinet
de consultants Deloitte voulait étudier
les propriétés d’un modèle financier. Et
le consortium Gocad, intéressé par la
prospection pétrolière, cherchait des
solutionspourdel’imageriedu sous-sol.
Face àeux, de jeunes volontaires
répartis en quatre groupes ont d’abord
écouté,puis se sont organisés pendant
trois jourset demi,avant delivrer le fruit
de leurs réflexions le cinquième et der-
nier jour. «Cette semaine doit montrer
qu’il est possible de faire des maths pous-
sées en entreprise. Il n’y anipromesses de
réussites, ni contrats àl’issue. C’est un
moyen de rapprocher deux mondes, aca-
démique et industriel », résume Céline
Lacaux, enseignante àl’ENSMN, coorga-
nisatricedecet événement soutenu par
l’Agence pour les mathématiques, en
interaction avec les entreprises et la
société(Amies) et le Groupement de
recherchemathsetentreprisesduCNRS.
«Debonnes idées sont sorties, mais
une semaine, c’est court. Certaines pistes
seront àtester, d’autres àraffiner, esti-
me GabrielFricout, d’ArcelorMittal. Ils
ont eu des regards neufs, différents de ce
que nous avions pu porter. »
«J’avaisunedreamteam avec des spé-
cialistes de simulations numériques, de
phénomènes stochastiques, ou d’appro-
ches mathématiques sur des phénomè-
nes physiques. Leur travail m’a fait
gagner beaucoup de temps», constate
Alan Picone de Deloitte.
«Jesuis très contente, carnousnesom-
mes pas habitués àcetravail en groupe
en maths. Et puis faire quelque chose qui
peut être utile en entreprise est intéres-
sant aussi », observe Laura Vincken-
bosch, en post-doc au centre de recher-
che Inria de Nancy.
De telles initiatives sont récentes en
France,alors qu’elles sont courantes en
Allemagne et en Grande-Bretagne
depuis des dizaines d’années. «Malgré
l’excellence des mathématiciens fran-
çais, les relations entre les entreprises et
le monde académique ne sont pas assez
développées», regrette Georges-Henri
Cottet, président de l’Amies, née en
2011 de ce constat et financée par les
Investissements d’avenir àhauteur de
500000euros par an.
Il est pourtant évident que les maths
peuvent aussi être «utiles ». Des sec-
teurs traditionnels comme l’automobi-
le, l’aérospatial ou la finance l’ont
depuis longtemps compris. Modéliser
des structures, des fluides, des aléas…
demande des compétences scientifi-
ques élevées. «Denouveaux besoins
émergent aussi, comme dans le secteur
des big data, ces masses de données qu’il
s’agit de stocker et analyser au mieux. En
outre, beaucoup d’instrumentsde mesu-
res demandent àembarquer des systè-
mes intelligents de traitement du signal.
Pour être compétitif, il faut avoir ses pro-
pres méthodes», décrit M. Cottet.
Le message commence àpasser. En
janvier, àParis, le deuxième forum
Emploi-maths aété fréquenté par
1300 personnes, 30 %deplus que l’édi-
tion précédente. L’Amies dispose de
sept «facilitateurs»dans différentes
régions pour aider les contacts entre
laboratoires et entreprises, notam-
ment les PME. Cela peut déboucher sur
des stages, des contrats ou tout simple-
ment des accès àdes plates-formes aca-
démiques de calculs scientifiques. Un
inventaire de ces relations nouvelles
sera terminé cette année.
«Les entreprises commencent àse
rendre compte de la maturitéet de l’ingé-
niosité des docteurs », insiste Céline
Lacaux. «Leproblème est souvent de
convaincre les mathématiciens que,
même sur des temps courts, on peut fai-
re des choses intéressantes. Inverse-
ment, il faut convaincre les dirigeants
que les maths ne sont pas seulement
l’outil de sélection qu’ils ont connu pen-
dant leurs études, mais que cela peut
être un outil opérationnel efficace»,
conclut Georges-Henri Cottet.
p
David Larousserie
Quand l’industrie mise sur les équations
Pendant une semaine, des jeunes mathématiciens ont planché sur des problèmes soumis par des entreprises
D
ifficile d’échapper au cliché
dusavantfouquand on pen-
se aux mathématiciens. «Il
yaplusieurs formes possibles de
folie qui peuvent être attachées aux
scientifiques, mais les mathémati-
ciens ne semblent pas concernés par
les figures de la démesure et des
expériences contre nature àlaFran-
kenstein, qui sont plutôt accolées à
des physiciens ou des biologistes,
constatePierreCassou-Noguès,pro-
fesseur au départementde philoso-
phie de Paris-VIII. Dans le cas des
mathématiciens, on va plutôt trou-
ver des figures de personnes en
retrait de lasociété ou ayant de vrais
problèmes mentaux.»
Les exemples ne manquent pas,
eneffet.Récemment,le Russe Grigo-
ri Perelman, après un travail inten-
se et solitaire, adémontré un résul-
tat important en topologie géomé-
trique, la conjecture de Poincaré. Ce
qui lui valut en 2006 la médaille
Fields, l’une des récompenses les
plus prestigieuses, et en 2010 le
Prixdu millénaire(assorti d’un mil-
lion de dollars) décerné par l’Insti-
tut de mathématiques Clay. Il les
refusa tous les deux et se retira de la
vie scientifique.
Auparavant, l’un de ses aînés,
Alexander Grothendieck, apatride
formé et travaillanten France, avait
adopté la même attitude de retrait.
Récompensé par la médaille Fields
en1966,il finit parquitter lemonde
académique au milieu des années
1980 pour s’isoler àlacampagne.
D’autres de leurs collègues ont
vraimentsouffertde maladiesmen-
tales. La bande dessinée Logicomix,
qui raconte l’histoire de la logique,
en est pleine. Ainsi de Gottlob Frege
(1848-1925), qui devint paranoïa-
que. Ou du plus célèbre, Georg Can-
tor (1845-1918), qui définit la théo-
rie des ensembles
et chercha à
caractériser
la notion
d’infini.
Il mourut
en hôpital psychiatrique. Enfin,
Kurt Gödel (1906-1978), autre logi-
cien célèbre, notamment pour des
théorèmes fondamentaux sur la
structure même d’une théorie
mathématique. Il mourut amaigri,
ayant refusé de s’alimenter par
peur d’un empoisonnement.
Cette «épidémie»touche en fait
unediscipline particulière,aux fron-
tières de la science et de la philoso-
phie.Touscessavants,en jetantau
début du XXesiècle les bases
d’une logique nouvelle, ont
aussiplongédansles tréfonds
de leur matière et de la rai-
son.Cela peutnepas lais-
ser indemne. «Dans le
cas de Gödel, il est intéres-
sant aussi de voir comment
la folie et la logique se
mêlent. Ainsi, sa théorie le
conduit àdémontrer l’im-
mortalité de l’âme et la possibili-
té du diable », explique Pierre
Cassou-Noguès, également auteur
des Démons de Gödel (Seuil, 2007).
Ce dernier cite aussi le cas de
l’Américain Emil Post (1897-1954),
qui, àl’instar d’Alan Turing, a
réfléchi àlanotion de calculabilité.
Bien qu’ils fussent arrivés tous
deux àdes résultats semblables,
Emil Post essaya de démontrer que
Turing avait tort. De cette obses-
sion, il développera une vision ori-
ginale du fonctionnement de l’es-
prithumain,dans laquelle ilest dif-
ficile de séparer folie et raison.
Serait-celetribut àpayeràlacréa-
tion? «Iln’y aguère plus de fous en
maths qu’il n’y en aenmusique ou
en peinture. Les cas célèbres sont un
peu les héros de notre mythologie»,
estime Cédric Villani. «Cen’est pas
quand on est fou qu’on est le plus
productif. Car il faut pour cela des
facultés de raisonnement logique »,
conclutlemathématicien
.p
D. L.
La logique, antichambre de la folie?
«Malgré l’excellence
des mathématiciens français,
les relations entre entreprises
et monde académique ne
sont pas assez développées »
Georges-Henri Cottet
président de l’Amies
Fine tranche
de glace
créée dans
un tunnel
de givrage
afin d’étudier
les transitions
de phase.
«INTERNATIONAL
JOURNAL OF HEAT AND
MASS TRANSFER »,
ELSEVIER, 1999.
Cette «épidémie »
touche une discipline
particulière, aux
frontières de la science
et de la philosophie
IV 0123
Vendredi 22 mars 2013