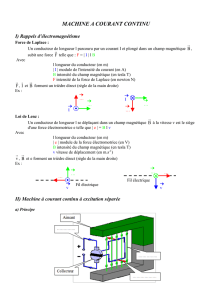
Retour sur le rail de Laplace

Retour sur le rail de Laplace
!"#$%&#%"#$'()%$%"&#("#*+,,%#
$-&+../0(%#1+"2#("#34+$5#6#("/7',$%#
#
8"#3'(,+"&#9#3/,3(.%#1+"2#.%#3/,3(/&:#
#
;"#%<%&#=#
#
>%2#-.%3&,'"2#./*,%2#1+"2#.%#
3'"1(3&%(,#2'"&#2'($/2#?#("%#7',3%##
#
#
#
@(/#.%2#$%&#%"#$'()%$%"&:#
#
A+"2#.%#,-7-,%"B%.#2%#1-5.+C+"&#?#.+#
)/&%22%#DE#/.#%F/2&%#1'"3#("%#7',3%#1%#
"+&(,%#-.%3&,/0(%E#0(/#$%&#%"#
$'()%$%"&#.%2#34+,G%2#
#

Transformation du champ par changement
de repère galiléen
H'/&#("#,-7-,%"B%.#IJ#%"#$'()%$%"&#5+,#,+55',&#?#I#+)%3#("%#)/&%22%#D:#
#
>J%F5,%22/'"#1%#.+#7',3%#K'(#1%#.J+33-.-,+B'"L#1'/&#M&,%#/")+,/+"&%#5+,#34+"G%$%"&#1%#
,-7-,%"B%.#/"%,B%.:#;F5,/$'"2#.J-G+./&-#1%#.+#7',3%#1%#>',%"&N#1+"2#.%2#1%(F#,-7-,%"B%.2#=#
O(/2#.+#.'/#1%#3'$5'2/B'"#G+./.-%""%#1%2#)/&%22%2#=#
!"#%"#B,%#
@(/#1'/&#M&,%#),+/%#5'(,#&'(&%#)/&%22%#):#!"#%"#1-1(/&#.+#&,+"27',$+B'"#1(#34+$5#
-.%3&,'$+G"-B0(%#5+,#34+"G%$%"&#1%#,-5P,%#Q+./.-%"#=#

Le champ électromoteur
8"%#3'"2-0(%"3%#54R2/0(%#%2&#1'"3#0(%#2/#'"#1-5.+3%#("#3'"1(3&%(,#+)%3#("%#)/&%22%#D#
1+"2#("#34+$5#$+G"-B0(%#6E#.%2#-.%3&,'"2#1%#3%#3'"1(3&%(,#)%,,'"&#("#34+$5#
-.%3&,/0(%##
S%#34+$5#%2&#1/&#champ&électromoteur:#S'"&,+/,%$%"&#+(#34+$5#-.%3&,'2&+B0(%E#3%#
34+$5#"J%2&#5+2#?#3/,3(.+B'"#"(..%#2(,#("#3/,3(/&#7%,$-##
#
#
#
;&#2'"#,'&+B'""%.#%2&#1'"3#"'"T"(.#K/.#"%#1-,/)%#5+2#1J("#5'&%"B%.#23+.+/,%L:#
#
!"#1-U"/&#.+#force&électromotrice&(f.e.m)&1J("#3/,3(/&#$'*/.%#5.'"G-#1+"2#("#34+$5#
$+G"-B0(%#3'$$%#.+#3/,3(.+B'"#1(#34+$5#-.%3&,'$'&%(,#2(,#3%#3/,3(/&&
S%V%#7:%:$#%2&#4'$'GP"%#?#("%#&%"2/'"#KD'.&2L:#!"#
5%(&#.+#$'1-./2%,#3'$$%#("#G-"-,+&%(,#1+"2#.%#3/,3(/&:#

Roue de Faraday
!"#7+/&#&'(,"%,#.%#1/20(%#?#.+#$+/"#+)%3#("%#
5(.2+B'"#W#=#.J+$5'(.%#2J+..($%#X#
#
S+.3(.'"2#.+#7:%:$#1+"2#.%#3/,3(/&#=#
>+#)/&%22%#1J("#5'/"&#Y#1(#1/20(%#)+(&##
>%#5,'1(/&#)+(&#
;&#1'"3#
>%#3'(,+"&#/"1(/&#3/,3(.%#1%#!#)%,2#Z#K2%"2#1%#D#∧#6L:#@(%..%#%2&#.+#1/,%3B'"#1%2#7',3%2#
1%#>+5.+3%#[###
#
SJ%2&#("#,-2(.&+&#G-"-,+.E#0(/#2%,+#-"'"3-#3'$$%#!"#$%&#'(#$()*#