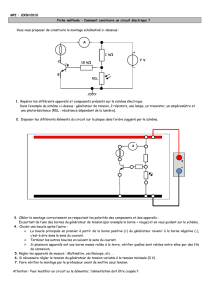
Telecharger - L`esprit des maths

TOPOLOGIE de la DROITE REELLE
peut se définir comme un corps totalement ordonné archimédien complet.
Nous ne donnerons pas ici de construction de

Une topologie sur un ensemble E est définie par l’ensemble des ouverts, qui sont des parties de E,
satisfaisant à des axiomes de stabilité par réunion et par intersection finie. Dans le cas de on
appelle ouvert toute réunion d’intervalles ouverts (et dans le cas de
, toute réunion de pavés
ouverts, un pavé étant le produit cartésien de intervalles ouverts).
Montrer l’équivalence: est ouvert dans
Notion de Point d’Accumulation
On dit que est un point d’accumulation de l’ensemble si tout ouvert contenant contient au
moins un point de distinct de , et par conséquent une infinité de points de .
Théorème : tout sous-ensemble infini borné de
Notion de Point Adhérent
On dit que est un point adhérent à l’ensemble si tout ouvert contenant contient au moins un
point de .
Tout point de peut donc être considéré comme adhérent à , sans que l’on n’exige aucune
propriété topologique pour ce point ; en revanche, un point adhérent à sans être dans est
nécessairement un point d’accumulation de .
On verra en topologie générale que l’ensemble des points adhérents à un ensemble se définit
comme le plus petit fermé contenant , cet ensemble est noté . L’ensemble des points
d’accumulation de est parfois noté .
1
/
2
100%