2006-2009

UNIVERSITE DE LIEGE
EXAMEN D’ADMISSION AUX ETUDES
D’INGENIEUR CIVIL
G´eom´etrie et g´eom´etrie analytique
Enonc´es et solutions des examens de 2006, 2007, 2008
et 2009 (premi`ere session)
1

1 Enonc´es
Pour chaque examen, on demande de r´esoudre trois questions parmi les cinq
qui sont ´enonc´ees.
1.1 Examen de juillet 2006
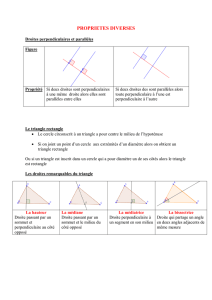
1. Par un point Aext´erieur `a un cercle C, on m`ene les tangentes `a celui-ci,
qui rencontrent Caux deux points de tangence Bet B0.
Soient C0le cercle circonscrit au triangle ABB0et tla tangente `a C0
issue de B. La droite trencontre Cen Bet en un deuxi`eme point C.
(a) D´emontrer que le triangle CBB0est isoc`ele.
(b) D´emontrer que les hauteurs issues de Bdans les triangles ABB0
et CBB0ont la mˆeme longueur.
(c) D´emontrer que le centre du cercle inscrit au triangle AB0Cest
situ´e sur la droite BB0.
2. Soit ABC un triangle rectangle en Aet dune droite contenant A.
On note Gla projection orthogonale de Bsur det Ela projection
orthogonale de Csur d. On note ´egalement d1la parall`ele `a AC men´ee
par Get d2la parall`ele `a AB men´ee par E.
(a) D´emontrer que d1,d2et BC sont concourantes.
(b) D´eterminer le lieu g´eom´etrique du point d’intersection de d1et d2
quand dvarie.
3. Soit ABC un triangle d’orthocentre H. On note respectivement A1,
B1et C1les pieds des hauteurs issues de A,Bet C. On note |−−→ XY |la
longueur du vecteur −−→ XY . D´emontrer la relation
1
2(|−→
AB|2+|−−→ BC|2+|−→ CA|2) = −−→ AH.−−→ AA1+−−→ BH.−−→ BB1+−−→ CH.−−→ CC1.
4. Soit SABC un t´etra`edre tel que SA soit perpendiculaire `a ABC. On
note A0la projection orthogonale de Asur SBC. D´emontrer la relation
A(SBC)
A(ABC)=A(ABC) A(A0BC),
o`u A(XY Z) d´esigne l’aire du triangle XY Z.
2

5. On consid`ere un t´etra`edre OABC et on note Gle centre de gravit´e
de la face ABC. On note respectivement A1,B1et C1les milieux de
[B, C], [C, A] et [A, B]. Un plan πparall`ele `a ABC coupe OA,OB et
OC en respectivement A0,B0et C0.
(a) D´emontrer qu’il existe une unique position de πpour laquelle les
droites A0A1,B0B1et C0C1sont parall`eles `a OG.
(b) D´emontrer que pour toutes les autres positions, ces droites sont
concourantes en un point Pde la droite OG.
1.2 Examen de septembre 2006
1. Soient un cercle Cde centre Oet une corde [C, D] de ce cercle. Deux
droites non confondues d1et d2sont s´ecantes `a la corde [C, D] et ren-
contrent celle-ci en son milieu M. La droite d1rencontre Cen deux
points A1et B1, et la droite d2rencontre Cen A2et B2. On suppose
que les points A1et A2sont situ´es du mˆeme cˆot´e de la corde [C, D]. On
note Pl’intersection de [C, D] et de la droite A1B2, et Ql’intersection
de [C, D] et de A2B1. Le pied de la hauteur issue de Odu triangle
OA1B2(resp. OA2B1) est not´e H1(resp. H2).
(a) D´emontrer que les triangles A1H1Met A2H2Msont semblables.
(b) D´emontrer que les angles \ P H1M,\ P OM,\ MOQ et \ MH2Qsont
´egaux ou suppl´ementaires deux `a deux.
(c) En d´eduire que Mest le milieu du segment [P, Q].
2. On consid`ere un quadrilat`ere ABCD. Le milieu de la diagonale [A, C]
est not´e Pet celui de [B, D] est not´e Q.
D´emontrer la relation
|−→ AB|2+|−−→ BC|2+|−−→ CD|2+|−−→ DA|2=|−→ AC|2+|−−→ BD|2+ 4|−→ P Q|2.
3. Soient deux cercles Cet C0non concentriques. Etant donn´e un point P
du plan ext´erieur `a ces deux cercles et une tangente p`a Cissue de P,
on note P1le point o`u prencontre C. De mˆeme, on note P2le point de
tangence `a C0d’une tangente p0`a ce cercle issue de P.
D´eterminer le lieu g´eom´etrique des points Pdu plan tels que
|−−→ P P1|2− |−−→ P P2|2=k,
o`u kest un nombre r´eel donn´e.
3

4. On consid`ere un t´etra`edre ABCD dont la base BCD est ´equilat´erale,
et tel que la droite reliant Aau centre de gravit´e de cette base est
perpendiculaire au plan BCD.
Soient Pun point int´erieur au triangle BCD, et πet π0deux plans
s’appuyant sur la droite AP et respectivement parall`eles aux droites
BC et BD. Les plans πet π0rencontrent l’arˆete [C, D] en deux points
respectifs Qet R. Les distances du point Paux arˆetes [B, C], [B, D]
et [C, D] sont respectivement not´ees α,βet γ. La longueur de l’arˆete
[B, C] est not´ee δ.
(a) Montrer que le triangle P QR est ´equilat´eral.
(b) Exprimer la longueur d’un cˆot´e du triangle P QR en fonction de
α,βet δ.
(c) Montrer que la valeur de α+β+γne d´epend pas de la position
de P.
(d) En d´eduire que la somme des distances de Paux quatre faces du
t´etra`edre ABCD est ind´ependante de P.
5. On consid`ere une droite dde l’espace et un point Pn’appartenant pas `a
d. Pour tout plan πcontenant d, on note Xla projection orthogonale de
Psur π. D´eterminer le lieu g´eom´etrique d´ecrit par le point Xquand
πvarie. (Suggestion : Si l’on proc`ede par g´eom´etrie analytique, on
choisira un syst`eme d’axes o`u dest l’un des axes).
1.3 Examen de juillet 2007
1. Soit un cercle Ctangent int´erieurement `a un autre cercle C0, le point
de tangence ´etant not´e P. Par un point Qde C, on m`ene une tangente
`a Cqui rencontre C0en deux points Aet B.
D´emontrer que la droite P Q est la bissectrice d’un des angles form´es
par les droites P A et P B.
2. On consid`ere deux points distincts Aet Bdu plan et une droite d
perpendiculaire `a AB. On suppose en outre que l’intersection de det
AB n’appartient pas au segment [A, B]. Par Aon m`ene une droite d1
qui coupe den M. Par Bon m`ene une droite d2perpendiculaire `a d1.
On note Nl’intersection de det d2. D´eterminer le lieu du centre du
cercle circonscrit au triangle MNA quand d1varie.
4

3. On consid`ere un losange ABCD tel que le triangle BCD est ´equilat´eral,
et un point Pquelconque. D´emontrer que l’on a
|P A|2+|P C|2=|AB|2+|P B|2+|P D|2.
4. Soient αet βdeux plans perpendiculaires. Soient det d0deux droites
orthogonales entre elles telles que d⊂α,d0⊂β. D´emontrer que dou
d0est perpendiculaire `a α∩β.
5. Une sph`ere opaque de rayon ret de centre Cpos´ee sur un sol plan est
´eclair´ee par une source lumineuse ponctuelle O, situ´ee `a une distance
2rde Cet `a la mˆeme hauteur que C.
(a) D´eterminer le lieu des points de la sph`ere o`u les rayons lumineux
sont tangents `a cette sph`ere.
Suggestion : Utiliser la sym´etrie du probl`eme par rapport `a l’axe
OC.
(b) Caract´eriser la forme de l’ombre port´ee par cette sph`ere sur le sol.
1.4 Examen de septembre 2007
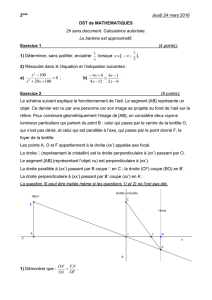
1. On consid`ere un triangle ABC du plan. On note Cle cercle circonscrit
au triangle et Ole centre de ce cercle. La bissectrice int´erieure de
l’angle ˆ Acoupe [B, C] en Det Cen I.
(a) D´emontrer que les droites OI et BC sont perpendiculaires.
(b) D´emontrer la relation
AB AC =AD 2+DB DC,
o`u XY d´esigne la longueur du segment [X, Y ].
2. Soient deux cercles Cet C0ext´erieurs l’un `a l’autre. D´eterminer le lieu
des points `a partir desquels les tangentes `a Cforment entre elles le
mˆeme angle que celui form´e par les tangentes `a C0. Pr´eciser la nature
de ce lieu.
3. On consid`ere un triangle ABC, et un point Parbitraire appartenant `a
son cˆot´e [B, C], distinct de Bet C. D´emontrer que la valeur de
−→
AB2
−−→
BC.−−→ BP +−→
AC2
−−→
CB.−→ CP +−→
AP 2
−→
P C.−−→ P B
est ind´ependante de Pet des dimensions du triangle.
5