Exercice 1 – Tracé de rayons

OPTICS II
Section de Physique
Cours: Pr. Romuald Houdré
Exercices: Nicolas Descharmes
Série 1
Rappels d’optique géométrique
20 février 2012
Exercice 1 – Tracé de rayons
Cas 1: Optique de relais
Une optique de relais (faible grandissement, distances objet-lentille et lentille-image
comparables) se compose généralement de deux lentilles convergentes tels que le centre de la
lentille L1 et le foyer de la lentille L2 sont confondus. Tracer l’image de l’objet
€
AB
à travers le
système suivant. Que vaut le grandissement lorsque
€
AB
se trouve dans le plan focal objet de L1 ?
Cas 2: La loupe
Le modèle optique le plus simple d’un œil consiste en une lentille convergente pour le cristallin et
d’une surface collectrice pour la rétine. Une loupe permet d’obtenir une image grossie d’un objet
lorsqu’elle est placée entre l’objet et le cristallin. Tracer l’image de l’objet
€
AB
obtenue sur la
rétine à travers le système loupe + cristallin. De quel type est l’image intermédiaire de
€
AB
à
travers la loupe seule ? Exprimer le grandissement en fonction de
€
O
1A
et
€
O
1F 1'

2
Cas 3: Le téléobjectif
Un téléobjectif se compose généralement d’une lentille (ou groupe de lentilles) convergente(s) et
d’une lentille (ou groupe de lentilles) divergente(s). Il permet d’obtenir une image agrandie
d’objets situés à longue distance. Faire le tracer de rayons pour un objet supposé à l’infini et de
taille angulaire α.
Exercice 2 – Points cardinaux
a) Soit un système optique centré que l’on considèrera dans le cadre du stigmatisme
approché (i.e. on fait l’hypothèse de l’approximation linéaire et tout système est
aplanétique). Ecrire la matrice de passage T(A1A1’) entre deux plans conjugués repérés
par A1 et A1’ sur l’axe optique. Montrer en particulier qu’un des coefficients est nul.
b) Exprimer cette matrice en fonction du grandissement transverse γt et du grandissement
angulaire γa (le milieu objet a pour indice n et le milieu image n’)
c) Montrer qu’un des quatre coefficients de la matrice est un coefficient caractéristique (noté
–V) non nul du système, i.e. il se conserve lors d’un changement de plan de référence.
d) On considère deux autres plans repérés par les points A2 et A2’ sur l’axe optique avec
€
d=A
1A2
et
€
"
d =A
1"A2"
. Calculer la matrice de transfert entre ces deux nouveaux plans. En
considérant que les points A2 et A
2’ sont conjugués, en déduire la relation générale de
conjugaison (on notera
€
V="
n
"
f
).
e) On définit les plans principaux comme étant les plans conjugués pour lesquels le
grandissement transverse γt vaut 1. Ces plans sont repérés sur l’axe optique par les points
principaux H (objet) et H’ (image). Ce sont les plans de référence d’un système optique.
Par rapport à ces plans il y a une expression particulière de la relation de conjugaison que
l’on déterminera (on utilisera la relation d’Abbe). Ecrire la matrice T(HH’)
f) Soient F et F’ les foyer objet et image. Déterminer
€
HF
et
€
"
H " F
.
g) Les points nodaux N (objet) et N’ (image) se définissent par γa=1. Déterminer
€
HN
et
€
"
H " N
.

3
h) Soit T(ES)=
€
A B
C D
"
#
$
%
&
'
la matrice de transfert d’un système optique entre les plans d’entrée
et de sortie repérés respectivement par les points E et S sur l’axe optique (ces plans ne
sont pas nécessairement conjugués). Déterminer
€
EH
et
€
S" H
(on utilisera la matrice
obtenue à la question d), en particulier la relation de passage entre les grandissements).
Important: Tout système optique se ramène à la connaissance de la position des points
cardinaux: points principaux (H et H’) et foyers (F et F’). La connaissance de H, H’, F et F’
permet la détermination de tous les rayons traversant le système.
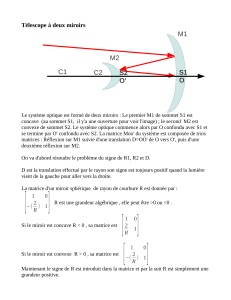
Exercice 3 (supplément) – Le télescope de Cassegrain
Un télescope de type Cassegrain est constitué de deux miroirs sphériques. Un miroir concave M1,
de sommet S1, centre C1 et de foyer F1, dit miroir primaire. Un miroir convexe M2, de sommet S2,
centre C2 et de foyer F2, dit miroir secondaire (voir figure).
Le miroir primaire est percé d’un trou en son sommet qui permet le passage de la lumière après
réflexions successives sur M1 et M
2. Les centres C1 et C 2 sont confondus : C1 = C2 = C. Les
diamètres d’ouverture des miroirs M1 et M2 sont notés respectivement 2a1 et 2 a2.
On se placera dans les conditions de l’approximation de Gauss.
1. Déterminer la position du foyer principal image F’ de l’objectif Cassegrain. On donnera
l’expression de la mesure algébrique
€
CF '
en fonction de
€
R
1=CS1
et
€
R2=CS2
2. Quelle relation existe-t-il entre R1 et R2 pour que le foyer principal image F’ se trouve au
sommet S1 de M1 ?
On considérera que cette relation est vérifiée dans toute la suite du problème.
3. On considère un rayon incident parallèle à l’axe optique. Ce rayon rencontre M1 à son
extrémité (y = a1). Déterminer l’angle que forme le rayon réfléchi issu de M1 avec l’axe

4
optique. En déduire le diamètre d’ouverture minimum 2a2 de M2 pour que tout faisceau
collecté par M1 soit ensuite défléchi par M2.
4. Exprimer l’angle maximal formé par un rayon issu de M2 avec l’axe optique. En déduire
la résolution théorique du télescope en fonction de a1 et R
1. On prendra les valeurs
suivantes : a1 = 1.2m, R1 = 11m, λobservation = 1µm.
5. Dans les faits, les turbulences atmosphériques limitent la résolution effective d’un
télescope de ce type à environ 50 µm. Quel est alors le diamètre « effectif » du télescope ?
Proposer une solution pour éviter ce problème.