M1 M2 C1 C2

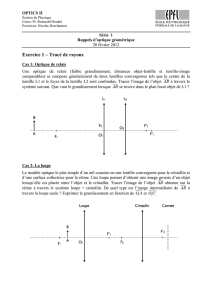
Télescope à deux miroirs
Le système optique est formé de deux miroirs : Le premier M1 de sommet S1 est
concave (au sommet S1, il y'a une ouverture pour voir l'image) ; le second M2 est
convexe de sommet S2. Le système optique commence alors par O confondu avec S1 et
se termine par O' confondu avec S2. La matrice Moo' du système est composée de trois
matrices : Réflexion sur M1 suivie d'une translation D=OO' de O vers O', puis d'une
deuxième réflexion sur M2.
On va d'abord résoudre le problème du signe de R1, R2 et D.
D est la translation effectué par le rayon son signe est toujours positif quand la lumière
vient de la gauche pour aller vers la droite.
La matrice d'un miroir sphérique de rayon de courbure R est donnée par :
[
1 0
−( 2
R)1
]
R est une grandeur algébrique , elle peut être >0 ou <0 .
Si le miroir est concave R < 0 , sa matrice est
[
1 0
2
R1
]
Si le miroir est convexe R > 0 , sa matrice est
[
1 0
−( 2
R)1
]
Maintenant le signe de R est introduit dans la matrice et par la suit R est simplement une
grandeur positive.
C1 C2 S2
O'
S1
O
M1
M2

Dans notre cas M1 est concave et M2 est convexe, la matrice du système est alors :
Moo' =
[
a11 a12
a21 a22
]
=
[
1 0
2/R11
]
[
1−D
0 1
]
[
1 0
−2/R21
]
=
[
1+2D
R2
−D
2
R1
−2
R2
+4D
R1R2
1−2D
R1
]
On veut étudier ce système pour que son point focal image F' soit confondu avec S1
c-à-d O. Cela veut dire tous simplement que O'F' soit positif et egal à S2S1 = D.
Or O'F' peut être extrait de la matrice par la relation :
O'F' =
a22
a21
= D =
(1−2D
R1
)R1R2
(2R2−2R1+4D)
pour
R2=k R1 , 0<k<1
k=−2D(2D−R1)
(R1(4D−R1))
Dans la pratique D est légèrement inférieur à
f1=R1
2
.
Télescope de Newton.
C1
S
F
α

1)L'objet AB qui est à l'infini, fait un angle α avec l'axe optique, (on dit qu'il est vu sous
un angle α .) sa hauteur est y. Son image
A1B1
de hauteur y' est sur le foyer F . Cette
image sera vu sous un angle β . Le rayon vient de AB et fait une translation de X après
il y a une réflexion sur le miroir concave suivie d'une translation de Y=SF. La matrice de
transfère de AB vers
A1B1
est :
M =
[
1−X
0 1
]
[
1 0
2/R1
]
[
1−Y
0 1
]
=
[
1−2X
R−X−Y+2XY R
2/R1−2Y
R
]
on écrit aussi
[
y
α
]
=
[
1−2X
R−X−Y+2XY R
2/R1−2Y
R
]
[
y '
β
]
Si
A1B1
est l'image de AB alors le terme
−X−Y+2XY
R
doit être nul.
Comme
X⇒∞
,
Y=R
2
. La relation entre
y
α
et
y '
β
devient :
[
y
α
]
=
[
1−2X
R0
2
R0
]
[
y '
β
]
→
α= 2
Ry '
y '=αR /2
= 9 mm
Le terme
1−2X
R
tend vers une valeur négative
⇒y '
y<0⇒
y' < 0.
2) Le miroir plan est placé entre S et F au point S2. Sa fonction est de donner une
image
A2B2
de
A1B1
symétrique par rapport au plan du miroir . Ensuite pour
voir cette image on utilise une lentille L de distance focale f0 et on déplace la
lentille jusqu'à ce que l'image
A2B2
soit sur le point focal objet de la lentille L.
La distance entre la lentille est l'axe optique est y= f0 +d . d est alors la distance

de
A2B2
au point S2 du miroir plan ce qui donne A1S2 = S2A2 =d .
Comme f0 = 2cm alors d = 10 cm et S2S1 = 90 cm.
Un télescope a pour but d'agrandir l'image de petits objets mais surtout de « séparer » les
images des objets très rapprochés donc d'augmenter l'angle sous lequel on voit ces
objets.
La relation entre l'objet et son image (Miroir sphérique, miroir plan, lentille L) :
[
y
α
]
=
[
A11 A12
A21 A22
]
[
y '
α '
]
doit respecter la condition
A21=0
pour un télescope.
Dans ce cas on a G =
1/A22=α ' /α
.
Le début du système télescope commence par S1 miroir concave et se termine par la
lentille L. Entre S1 et la lentille L, le rayon de lumière subit un certains nombres de
transformations :
C1 S1
S2
F
A1
B1
B2 A2
y
L
f0

Réflexion sur S1 concave
[
1 0
2/R1
]
=
[
1 0
1/f1
]
R et f sont des grandeurs positives
Translation de S1vers S2; S1S2 = DD
[
1−DD
0 1
]
Réflexion sur S2
[
1 0
0 1
]
Translation de S2 vers L ; S2L = y
[
1−y
0 1
]
Refraction à travers la lentille L convergente
[
1 0
1/fL1
]
La matrice totale est :
Mtélescope =
[
1 0
1/f1
]
[
1−DD
0 1
]
[
1 0
0 1
]
[
1−y
0 1
]
[
1 0
1/fL1
]
=
[
1−(DD+y)
fL
−(DD+y)
1
fL
+1
f−(DD+y) ff L
1−(DD+y)
f
]
le terme
1
fL
+1
f−(DD+y) ff L
=0⇒fL+f=DD+y
le grossissement angulaire est
G=1
A22
=f
(f−(DD+y))=−f fL
=α '
α.
Finalement
G=−f
fL
=−50
et α'= -0.45 rad.
L'image finale est renversée.