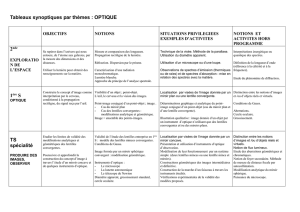
PCSI1 Exos Optique 2: Systèmes centrés 9697

PCSI1 Exos Optique 2: Systèmes centrés (approx de Gauss) 1112
1. Utilisation des formules:
Soit un miroir convergent de rayon de courbure R=30 cm . Un objet est placé 10 cm devant le centre C. Trouver
la position de l’image et le grandissement par 5 méthodes différentes ( 3 méthodes analytiques et 2 méthodes
graphiques).
2*. Champ angulaire d’un miroir:
Un observateur place son oeil à distance D devant un miroir de diamètre d. Etant donné que la pupille a un
diamètre très faible, on assimilera celle-ci à un point A’ placé sur l’axe du miroir.
Dans les 3 cas suivants, préciser la valeur de l’angle qui caractérise la portion d’espace accessible à la vision ( le
champ du miroir):
a) le miroir est plan
b) le miroir est convexe de rayon R
c) le miroir est concave de rayon R. Dans tous les cas , on a D < R/2.
3. Grandissement.
Faire une construction géométrique permettant de déterminer les points conjugués dans un grandissement
donné,  = 2 par exemple. On considérera les deux cas : lentilles convergentes ou divergentes. Vérifier à l’aide
des formules.
4. Elargisseur de faisceau.
Un faisceau lumineux quasi parallèle de diamètre d = 2 mm est issu d’un laser. On désire multiplier ce diamètre
par 10.
a) L’élargisseur utilise une lentille divergente et une lentille convergente de f’2 = 50 mm.
Calculer f’1 et la distance d qui sépare les deux lentilles.
b) Les deux lentilles sont convergentes et f’2 = 50 mm . Idem.
5. Distance minimale:
Rechercher la distance minimale objet réel / image réelle obtenue à l’aide d’une lentille convergente de distance
focale image f’.
6. Projecteur de diapositives
On désire projeter à l’aide d’une lentille mince une diapositive 24*36mm sur un écran placé à 4m de celle-ci
avec un grandissement de 100.
Quelle doit être la distance focale de la lentille utilisée et où doit-on placé celle-ci?
7. Etude d’un doublet.
Les doublets sont des systèmes centrés constitués de deux lentilles
minces L1 et L2 que l’on caractérise par trois nombres entiers (positifs
ou négatifs ) m, n, p tels que
f f
1 2
me n p u
où u est l’unité de
longueur du doublet.
On se propose d’étudier le doublet de Huygens ( 3, 2, 1 ) qui est
souvent utilisé pour réaliser un oculaire.
Déterminer graphiquement les foyers objet et images de ce doublet. En déduire la vergence du doublet.
L1 L2
O1 O2
e