Chapitre 7: travail et énergie I.TRAVAIL D`UNE FORCE

1
Chapitre 7: travail et énergie
Objectifs :
 Savoir établir l'expression du travail de la
force de pesanteur.
 Savoir établir l'expression du travail de la
force électrique dans un champ uniforme.
 Savoir établir l'expression du travail d'une
force constante.
 Savoir établir l'expression du travail de la
force de frottements (d'intensité constante
au cours d'un trajet rectiligne).
 Savoir analyser les transferts d'énergie au
cours d'un mouvement.
I.TRAVAIL D'UNE FORCE CONSTANTE
Un solide soumis à une force dont le point
d'application se déplace peut :
 être mis en mouvement (exemple : shoot
dans un ballon de foot) ;
 changer d'altitude (exemple : bille qui
tombe) ;
 se déformer temporairement ou
définitivement (exemple : les oscillations
d'un ressort ou une voiture lors d'un
accident) ;
 voir leur température s'élever (exemple :
disques de frein lors d'un freinage).
Dans tous ces cas, on dit que la force fournit un
travail.
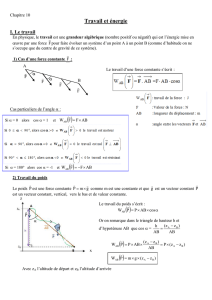
1) définition
Soit une force
F
constante appliquée entre les
points A et B.
Le travail de cette force entre le point A et B,
notée WAB
)F( 
est égal au produit scalaire du vecteur déplacement par le
vecteur force:
)AB,Fcos(.AB.FAB.F)F(
AB
W
=F.AB.cos()
Unités : WAB (
F
) en joule (J), F en Newton(N), AB en mètre (m).
2) Travail moteur, travail résistant
Lorsque le système reçoit du travail d'une force extérieure, alors ce
travail est positif, il s'agit d'un travail moteur.
Lorsque le système fournit du travail au milieu extérieur alors le travail est négatif, il s'agit d'un
travail résistant.
3) travail du poids
Sur une zone étendue à quelques kilomètres, on peut considérer le vecteur poids est une force
constante.
La valeur du poids P = m.g.
La grandeur g dépend de l’altitude et de la latitude.
Pour un déplacement de quelques kilomètres on peut considérer que g = constante.
*****************************************************************************************
α
valeur du travail
travail
moteur ou
résistant?
α
=0
0AB.F)αcos(.AB.F
AB
W
travail
moteur
2
π
α0
0)αcos(.AB.F
AB
W
travail
moteur
2
π
α
0)αcos(.AB.F
AB
W
travail nul
πα
2
π
0)αcos(.AB.F
AB
W
travail
résistant

2
Exemple : Solide sur un plan incliné.
Considérons un mobile autoporteur de masse m = 400 g se déplaçant sur un plan incliné d’un angle β
= 26,2 ° par rapport à l’horizontale.
1. Que peut-on dire du travail de la force , réaction du support sur le même trajet AB ?
2. Donner l’expression du travail du poids sur le trajet AB.
3. Utiliser le fait que le vecteur est une force constante.
4. En déduire l’expression du travail du poids sur le trajet AB en fonction de la dénivellation h
entre les positions A et B du mobile.
5. Le travail du poids sur le trajet AB est-il moteur ou résistant ?
On choisit un axe vertical Oz, vertical, orienté vers le haut et d’origine O.
Lorsque le mobile occupe la position A, il a l’altitude z A et lorsque il occupe la position B, il a l’altitude
z B.
6. Exprimer le travail du poids sur le trajet AB en fonction de z A et z B. Conclusion.
7. Calculer la valeur du travail du poids sur le trajet AB sachant que AB = 10,0 m.
Corrigé :
1. Le travail de la force , réaction du support, sur le même trajet AB est nul car la réaction du
support est perpendiculaire au support. Les frottements sont négligeables (mobile
autoporteur)
2. Expression du travail du poids sur le trajet AB.
3. On va utiliser deux propriétés du poids :

3
- La direction du poids est la verticale du lieu et la valeur du poids est constante.
- Le poids est une force constante.
4. On choisit le chemin suivant : AH et HB.
Avec h = AB . cos α
5. Le travail du poids sur le trajet AB est un travail moteur :
6. Pour donner le travail du poids en fonction de z A et z B, il faut donner l’expression des
vecteurs et en utilisant l’axe Oz et le vecteur unitaire .
On peut écrire que :
(1)
(2)
En conséquence :
Conclusion : Lorsque le centre de gravité G d’un corps passe d’un point A à un point B, le travail du
poids ne dépend que de l’altitude z A du point de départ et de l’altitude z B du point d’arrivée :
Le travail du poids ne dépend pas du chemin suivi.
Si le travail d’une force est indépendant du chemin suivi, c’est-à-dire s’il ne dépend que des
positions du point de départ A et du point d’arrivée B, on dit que la force est conservative.
Le poids est une force conservative.

4
Une force est conservative si le travail de cette force est indépendant du chemin suivi, c’est-à-
dire s’il ne dépend que des positions du point
de départ A et du point d’arrivée B.
Remarques :
Si z A > z B, l’altitude du point G a diminué :
le travail du poids est moteur.
Si z A < z B, l’altitude du point G a augmenté :
le travail du poids est résistant.
Si z A = z B, l’altitude du point G n’a pas
changé : le travail du poids est nul.
Pour déterminer la valeur du travail du
poids, on peut utiliser la relation
suivante :
Attention au signe ! Pour utiliser cette relation, il
faut savoir si le travail est résistant ou
moteur :
- Si le travail est moteur :
- Si le travail est résistant, alors :
Le travail du poids ne dépend pas du chemin suivi (voir figure ci dessus) mais uniquement de
l'altitude initiale et de l'altitude finale: on dit que le poids est une force conservative.
Remarque : le travail des forces de frottements dépend du chemin suivi, une force de frottement
n’est pas conservative.
*****************************************************************************************
3) Travail d'une force électrostatique conservative
a) Expression du travail de la force électrostatique.
Considérons une particule de charge q, assimilée à un point matériel M, qui se déplace d’un point
A à un point B dans un champ électrostatique uniforme .
Dans un champ électrostatique uniforme , la particule M est soumise à une force
électrostatique constante :
Expression du travail de la force électrostatique sur le trajet AB ?
Schéma : On considère le cas où la charge q > 0 pour pouvoir représenter la force .

5
- Lorsque la particule, de charge q se déplace du point A
au point B, dans l’espace où règne le champ électrostatique
uniforme , le travail de la force électrostatique est donnée
par la relation :
Avec ℓ = AB . cos α
b)- Différence de potentiel.
Par définition, la différence de potentiel entre deux points M et N placés dans un champ
électrostatique uniforme est donnée par la relation :
- cette différence de potentiel dépend du champ
électrostatique uniforme et des positions des points M et N.
c) Retour sur l’expression du travail de la force
électrostatique :
Autre expression du travail de la force électrostatique :
d)- Conclusion :
- Une particule de charge q, placée dans un champ électrostatique est soumise à une
force .