Le potentiel électrique

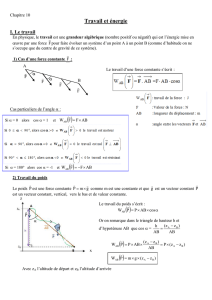
Le potentiel électrique
La force de Coulomb est conservative:
B
AB 12
A
W F .dl
B
B
AA
r
r
AB B A
rr
W F(r)dr P(r) P(r ) P(r )   
12 2
0
qq 1
Avec:F(r) 4r
r
12
AB 0 B A
q q 1 1
W = -
4πε r r

Le potentiel électrique
La force de Coulomb est conservative,
donc il existe une énergie potentielle électrique :
BE
A
U U(B) U(A) F .dl     

mais le signe de Udépend du signe des charges. Exemple :
U = U(B) –U(A) = –q E d
q > 0  U < 0 U(B) < U(A)
q < 0  U > 0 U(B) > U(A)

donc, on travaille avec :
Le potentiel électrique :
La différence de potentiel entre deux points de l'espace est définie par :
U
Vq
Unité de potentiel du S. I. :
le volt (V)
1 V = 1 J / 1 C

U = U(B) –U(A) = –q E d
q > 0  U < 0 U(B) < U(A)
q < 0  U > 0 U(B) > U(A)
V= U / q = –q E d / q = –E d
ne dépend pas de la charge et donc de son signe:
 V < 0 V(B) < V(A).
La plaque positive est toujours à un potentiel électrique plus élevé que
la plaque négative, quelle que soit le signe de la charge considérée !
Energie potentielle et potentiel électrique de 2 plaques chargées:
Energie potentielle:
Potentiel (électrique):