Cours sur "Travail et Enérgie"

TRAVAIL ET ENERGIE
I- QUELS SONT LES EFFETS POSSIBLES D’UNE FORCE DONT LE POINT
D’APPLICATION SE DEPLACE ?
Dans cette introduction, on va exercer une force et modifier son point d’application afin de déplacer un objet
d’un point à un autre.
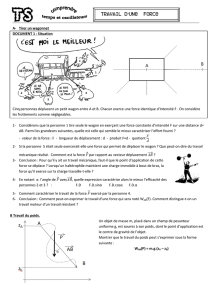
On agit sur le mouvement d’un wagonnet en approchant un sèche-cheveux .
1. Comparez l’efficacité de la force qui agit sur le mouvement du wagon selon la direction et le sens suivant
lesquels l’air est soufflé sur le wagon. Quelles sont les directions les plus efficaces pour accélérer le
wagon ? pour le freiner ?
2. Y a-t-il une ou des directions particulièrement inefficaces pour agir sur la vitesse du wagon ? Que peut-on
dire des directions intermédiaires ?
Lorsqu’une force constante
F
agit sur un mobile en mouvement de translation tout au long d’un déplacement
D
,
on dit qu’elle effectue un travail W. Selon les cas, un travail peut être « moteur » « résistant » ou « nul »
3. Dans quels cas diriez-vous qu’un travail est moteur ? résistant ? nul ?
4. Parmi les relations ci-dessous proposées pour définir le travail qu’une force constante de valeur F effectue
sur un mobile au cours d’un déplacement rectiligne de longueur D, quelle est celle qui vous paraît la mieux
convenir et pourquoi ?
DFW .
sin..DFW 
cos..DFW 
..DFW 
α = (
F
,
D
) représente l’angle entre le sens de la force et le déplacement du wagonet de la gauche vers la
droite
II- DEFINITION TRAVAIL D’UNE FORCE
Soit une force
F
constante appliquée entre les points A et B. Le travail de cette force entre le point A et B,
notée WAB
)F( 
est égal au produit scalaire du vecteur déplacement par le vecteur force:
WAB(
F
) =
F
.
AB
= F.AB.cos(
F
.
AB
) = F.AB.cos(
α
)
WAB (
F
) en joule (J), F en Newton(N), AB en mètre (m).
En fonction de la valeur de l’angle α, le travail sera moteur (α  90°), nul (α = 90°) ou résistant (α  90°)

III- EXPRESSION DE DIFFERENTS TRAVAUX
1) Travail du poids
Un objet de masse m passe de l’altitude yB à l’altitude yA.
L’objet est soumis à son poids
P
= - m.g.
j
et on a
AB
= (xB-xA)
i
+ (yB-yA)
j
- Calculer le travail du poids WAB(
P
)
- Que peut-on dire de ce travail si l’objet emprunte des chemins différents ?
- Dans quels cas le travail est moteur ? résistant ?
2) Travail de la force électrostatique
Rappel: entre 2 plaques chargées règne un champ électrique
E
orienté de la plaque positive vers la plaque
négative. La valeur du champ électrostatique entre 2 plaques P (plus) et N (négative) est égale à la tension UPN
divisée par la distance d entre les plaques:
d
PN
U
E
Unité: UPN(V) > 0, d(m), E (V.m-1) > 0
L’objet est soumis à la force
F
= q.E.
i
et on a
AB
= (xB-xA)
i
+ (yB-yA)
j
- Calculer le travail du poids WAB(
F
)
- Que peut-on dire de ce travail si l’objet emprunte des chemins différents ?
- Dans quels cas le travail est moteur ? résistant ?
Dans les 2 cas précédents, on dit que ces forces sont………………..car le travail……………………
3) Travail de la force de frottement
On considère un objet en mouvement sur une table et soumis à des frottements
f
- Calculer le travail du poids WAB(
f
) et WCD(
f
)
- Quel est la nature du travail ?
on dit que la force de frottement est ………………..car le travail………………………………

IV) ENERGIES ET TRAVAUX DES FORCES CONSERVATIVES
1) Forces conservatives et énergies potentielles
Généralisation: la variation d'énergie potentielle d'un système se déplaçant d'un point A à un point B est égale à l'opposé du
travail effectué par les forces conservatives entre le point A et le point B:
 )F(
AB
WEpp 
2) Conservation de l’énergie mécanique
L’énergie mécanique d’un système vaut Em = Ec + Ep
Où Ec est l’énergie cinétique définie par Ec =
2
1
m.v²et Ep l’énergie potentielle
Dans le cas où le système est soumis à des forces conservatives et/ou à des forces non-conservatives dont
le travail est nul, son énergie mécanique se conserve. On a donc Em = 0
Il y a donc transfert de l’énergie potentielle en énergie cinétique et inversement
Exemple : mouvement d’un objet sur un plan incliné sans frottement, pendule simple, pendule élastique…
l'animation étude énergétique du pendule
3) Non conservation de l’énergie mécanique
Dans la cas où le système est soumis au moins à des forces non conservatives qui travaillent, l’énergie mécanique
ne se conserve pas. On a :
Em = W(
f
non conservative)
Ce phénomène dissipatif est souvent dû aux frottements
Exemple : mouvement d’un objet sur un plan incliné avec frottement…'pendule amorti'
variation d'énergie potentielle de pesanteur Epp
et travail du poids
En première S, on définit l’énergie potentielle
de pesanteur d’un objet à l’altitude z par
l’expression Epp = m.g.z
Calculer la variation d’énergie potentielle de
pesanteur,Epp, entre un point de départ A et un
point d’arrivée B
En déduire une relation entre WAB(
P
) et Epp
variation d'énergie potentielle électrique et
travail de la force électrostatique
Par analogie, donner l’expression de l’énergie
potentielle électrique d’une particule de charge
q en un point de potentiel V
Epe=………………….
Calculer la variation d’énergie potentielle
électrique,Epe, entre un point de départ A et
un point d’arrivée B
En déduire une relation entre WAB(
F
) et
Epe