I – SPECTRES ATOMIQUES

I – SPECTRES ATOMIQUES
Quand le rayonnement émis par les atomes excités d’un tube à décharge ou d’un arc
électrique est dispersé à l’aide d’un prisme ou d’un réseau, le rayonnement peut être examiné
en fonction de la longueur d’onde, de la fréquence ou de l’énergie d’un quantum.
Tous les spectres obtenus de cette façon montrent que le rayonnement est formé de
plusieurs raies spectrales étroites qui apparaissent sur des diagrammes complexes. Elles sont
caractéristiques de l’élément et les atomes sont responsables de l’émission. Pour émettre le
spectre atomique, une substance doit contenir des atomes libres. Le spectre de l’atome
d’hydrogène est relativement simple et a été à la base des premières interprétations
théoriques.
Spectres
Sources lumineuses
On connaît deux types de sources lumineuses :
1. les sources thermiques : dans lesquelles un matériau est porté à haute température, comme c’est le cas du
tungstène dans les ampoules électriques à incandescence. Ce type de source a un spectre d’émission
continu. Ce spectre continu dépend essentiellement de la température.
2. Les sources lumineuses à décharge : dans lesquelles un courant électrique traverse la vapeur d’un élément
chimique donné.
Ces sources à décharge ont un spectre d’émission discret c’est à dire un spectre de raies bien définies comme
observées expérimentalement par le spectrographe. Ce spectre de raies est caractéristique des différents types
d’atomes ou types d’ions présents dans la vapeur.
Principe de combinaison et loi de Bohr
Ces fréquences d’émission caractéristiques de chaque atome, n’ont pu être interprété qu’après avoir découvert la
loi fondamentale qui relie les fréquences émises par un même atome.
Les longueurs d’onde des raies de l’hydrogène atomique sont données par la loi de Balmer-Rydberg :
, où R est une constante déterminée à partir des valeurs expérimentales appelée constante de Rydberg et n et p
sont deux nombres entiers. Si on exprime λ en cm la constante de Rydberg vaut : R=109 677 cm-1.
Cette loi a été généralisée à tous les atomes par Ritz en 1908 dans son principe connu sous le nom de Principe de
combinaison de Ritz : ‘ Les nombres d’onde 1 / λ des radiations émises par un même atome peuvent être
numérotés avec deux indices et exprimés comme les différences entre les termes d’une suite dépendant d’un seul
indice :
1 / λnp = Tn − Tp
Tn est appelé terme spectral. Bohr interprète cette loi en utilisant le langage des photons, il écrit :
C’est-à-dire que la loi de combinaison énoncée pour les nombres d’onde s’applique aussi à l’énergie hνnp des
divers photons émis par un même atome.

si on admet que chaque photon est émis par un seul atome isolé, l’énergie hνnp représente la perte d’énergie subie
par un atome au cours du processus d’émission ; et la loi de conservation de l’énergie exige que :
hνnp = Ei − Ef
Ei étant l’énergie initiale de l’atome avant émission et Ef l’énergie finale de l’atome après émission du photon
hνnp.
la comparaison des deux équations permet d’identifier les nombres hcTn et hcTp avec les valeurs de l’énergie
interne E de l’atome avant et après l’émission.
Bohr (en tenant compte de l’existence des photons), pour expliquer la loi de combinaison il a fait l’hypothèse
suivant : « L’énergie emmagasinée par un atome ne peut prendre que certaines valeurs particulières formant une
suite discontinue »
L’atome émet une onde de fréquence νnp lorsqu’il passe de l’état initial d’énergie Ep = − hcTp à l’état d’énergie
inférieur En = − hcTn et la loi de Bohr s’écrit :
hνnp = Ep − En
Expérience de résonance optique
On éclaire un ballon en verre contenant de la vapeur de sodium à l’aide d’une lampe à décharge à vapeur de
sodium. (On fait au préalable du vide dans le ballon qui contient un petit morceau de sodium que l’on chauffe
pour avoir de la vapeur de sodium). On observe :
1. le faisceau de lumière émergeant est atténué, une partie de son intensité a été absorbée par la vapeur.
2. La vapeur dans le ballon devient elle-même une source de lumière : elle émet dans toutes les directions de
l’espace une lumière de même longueur d’onde appelée lumière de résonance.
Figure: Expérience de résonance optique
La résonance optique est un cas particulier du phénomène de fluorescence. Le terme de fluorescence désigne
l’émission de la lumière par un corps lorsqu’il est irradié par un faisceau lumineux. La lumière émise en
fluorescence est en général de fréquence inférieure à celle de la lumière du faisceau primaire. Mais la lumière
émise dans la résonance optique a la même longueur d’onde que celle de la lumière du faisceau primaire.
On vérifie les lois générales suivants :
1. une vapeur monoatomique peut absorber fortement un faisceau lumineux seulement si la fréquence de
cette lumière coïncide avec celle d’une raie spectrale de l’atome constituant la vapeur.
2. seuls les fréquences de certains raies spectrales permettent d’observer cette absorption intense qui est
accompagnée d’une émission de fluorescence à la même fréquence.
L’interprétation de ce phénomène est facile à partir de l’hypothèse des niveaux d’énergie.
1. L’atome peut absorber les photons qui lui apportent exactement la différence d’énergie entre deux états
possibles En et Ep et lui permettent ainsi d’effectuer la transition du niveau inférieur En au niveau
supérieur Ep. Les photons absorbés obéissent à la loi de Bohr : hνnp = Ep − En.
2. il reste à expliquer pourquoi l’absorption se produit pour les fréquences de quelques raies spectrales à
l’exclusion des autres. L’atome reste stable à l’état fondamental. Si la vapeur à l’état normal contient
seulement des atomes à l’état fondamental E1, elle ne peut absorber que les photons capables de susciter
une transition à partir de cet état fondamental. C'est-à-dire correspondant à certaines raies spectrales
particulières : hν1p = Ep − E1. Dans le cas de l’hydrogène les raies de résonance sont les raies de la série de
Lyman.

3. L’émission s’explique par le fait qu’un atome qui a absorbé un photon passe dans un état excité. L’atome
excité tend à revenir spontanément à l’état fondamental en réémettant des photons ayant exactement la
différence d’énergie entre l’état excité en question et l’état fondamental.
Expérience de Franck et Hertz
L'expérience a pour objet de prouver la quantification des niveaux d'énergie des électrons dans les atomes. Elle a
ainsi permis de confirmer les hypothèses du modèle de l'atome de Bohr.
Principe
D'après la mécanique quantique, les électrons des atomes ne peuvent occuper que des niveaux d'énergie discrets.
L'absorption ou l'émission d'énergie se fait alors de manière discrète par des quanta d'énergie. Cette quantité
d'énergie correspond à la transition électronique, mais aussi à l'énergie transmise à une particule s'il s'agit d'une
diffusion inélastique. Afin de mettre en évidence la quantification des niveaux d'énergie, Franck et Hertz ont
cherché à montrer l'absorption de certains électrons. Pour être absorbés ces derniers doivent posséder une certaine
énergie correspondant à une transition électronique, autrement dit, à la différence d'énergie ΔE entre les niveaux
d'énergie final et initial. Pour l'absorption ou l'émission d'un photon, la différence d'énergie est :
ΔE = | Ef − Ei | = hν
où :
 Ef est l'énergie de l'état final,
 Ei l'énergie de l'état initial,
 ν la fréquence de raie spectrale, et h la constante de Planck.
Expérience
Résultats
Dans l'expérience, Franck et Hertz ont fait circuler un faisceau
d'électrons dans un tube à vide contenant du mercure gazeux. Pour y
arriver, ils ont utilisé une triode, c'est-à-dire un dispositif composée
d'une cathode, d'une grille polarisée et d'une anode.
Les électrons, émis de la cathode, peuvent alors entrer en collision
avec des atomes de mercure durant leur course entre la cathode et
l'anode. Il y a deux types de chocs :
 des chocs élastiques où il n'y a pas de transfert d'énergie des
électrons du faisceau avec les atomes de mercure percutés, et
les électrons gardent donc leur énergie,
 des chocs inélastiques, et dans ce cas, les électrons émis par
la cathode vont percuter les électrons de plus basse énergie des
atomes de mercure, et ceux-ci vont passer sur une orbite
d'énergie supérieure, suivant l'interprétation de Bohr.
La variation de courant reçu par l'anode est mesurée en fonction de l'énergie cinétique des électrons, et il est ainsi
possible d'en déduire les pertes d'énergie des électrons lors des collisions. L'ensemble de la triode est contenu à
l'intérieur d'une capsule en verre qui contient le mercure. Pour que les électrons soient arrachés et qu'ils aient une
vitesse suffisamment importante, une tension d'accélération est établie entre la cathode et la grille.

SPECTRE DE RAIES ET LA CONSTANTE DE RYDBERG
I. Introduction et objectifs
Lors d'une analyse spectrale, deux types de spectres peuvent être observés: un spectre continu et un spectre de
raies (spectre discret). Nous savons que les solides (de même que les liquides et les gaz denses) chauffés émettent
de la lumière ayant un spectre continu de longueurs d'onde. On suppose que ce rayonnement est dû aux
oscillations des atomes et des molécules, qui dépendent surtout de l'interaction entre chaque atome ou molécule et
ses voisins. Les gaz raréfiés aussi peuvent être excités de façon à émettre de la lumière. On atteint ce résultat par
un chauffage intense ou, plus couramment, par l'application d'une haute tension dans un tube à décharge
contenant le gaz à basse pression. Comme les gaz excités n'émettent de la lumière que de certaines longueurs
d'onde, l'analyse de cette lumière à travers la fente d'un spectroscope révèle un spectre de raies plutôt qu'un
spectre continu.
Les spectres de raies servent donc de clé pour comprendre la structure de l'atome: toute théorie de la structure
atomique doit permettre d'expliquer pourquoi les atomes émettent seulement de la lumière de longueurs d'onde
discrètes et doit pouvoir prédire ces fréquences.
Théorie
Les électrons sous agitation thermique dans une source de lumière incandescente émettent une radiation
électromagnétique (lumière) composée de différentes longueurs d'onde, produisant ainsi un spectre continu. En
analysant la lumière émise d'un gaz excité, d'un liquide vaporisé ou d'un solide, des lignes spectrales, comme
celles de la figure 1, sont observées.
Spectre visible de l'hydrogène.
La physique moderne explique ces spectres en termes de photons de lumière de longueurs d'onde discrètes émis
lors de transitions entre deux niveaux d'énergie. Chaque substance possède un ensemble de raies spectrales de
longueurs d'onde bien déterminées.

APPLICATIONS
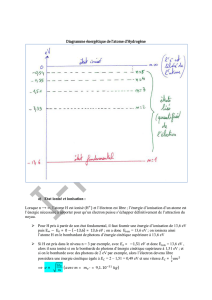
Voici le spectre de raies d’émission de l’hélium :
On remarque que celui-ci est composé de trois raies intenses :
Une raie bleue (B) de longueur d’onde 502 nm,
une raie jaune (J) à 588 nm,
et une raie rouge (R) à 668 nm.
1) Retrouvez à partir de ces trois raies, la valeur du quantum d’énergie auxquelles elles correspondent, et
remplissez le tableau ci-dessous (4) et (5) :
On utilise la formule pour trouver ΔE, puis on convertit ensuite l’énergie obtenue en eV.
Pour la radiation bleu :
Pour les autres radiations, voici le tableau :
Couleur
λ (en nm)
ΔE (en J)
Δ E (en eV)
Bleu
502
3,96 x 10-19
2,47
Jaune
588
3,38 x 10-19
2,11
Rouge
668
2,97 x 10-19
1,86
B
J
R
J
hc
E19
9
8-34 10*0.4
10*502 10*0.310*6.62 
eV
JenE
eVenE47.2
10*6.1 10*0.4 10*6.1 )(
)( 19
19
19 