5.cours.droites.triangles.08.

B
C
A
sommet
principal
base
Chapitre 9 : Droites remarquables d’un triangle.
I - Rappels : Médiatrice d’un segment, bissectrice d’un angle.
Définition : La médiatrice d’un segment est la droite perpendiculaire à ce segment et qui passe par son milieu.
Propriété :
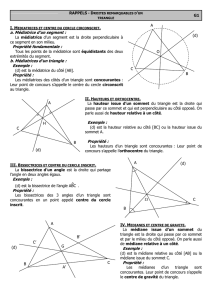
Dans un triangle, les médiatrices des trois côtés se coupent au centre du cercle circonscrit au triangle.
Définition : La bissectrice d’un angle est la demi-droite qui sépare cet angle en deux angles adjacents de même
mesure.
II - Médianes d’un triangle.
Définition : Dans un triangle, une médiane est une droite qui
passe par un sommet et par le milieu du côté opposé à ce
sommet.
Tracer la médiane issue de A
ou relative au côté [BC]
Théorème (admis) : Les trois médianes d’un triangle sont concourantes.
III - Hauteurs d’un triangle.
Définition : Dans un triangle, une hauteur est une droite qui passe
par un sommet et qui est perpendiculaire au côté opposé à ce
sommet.
Tracer la hauteur issue de A
ou relative au côté [BC]
Placer le point H, pied de la hauteur issue de A dans ABC.
Théorème (admis) : Les trois hauteurs d’un triangle sont concourantes.
IV - Triangles particuliers.
1) Triangle isocèle.
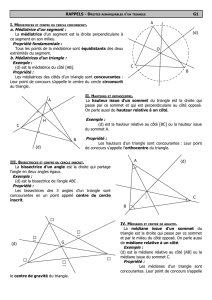
Théorème (admis) : Si un triangle est isocèle, alors la médiane, la
hauteur et la bissectrice issues du sommet principal, et la médiatrice
relative à la base sont des droites confondues.
2) Triangle équilatéral.
Théorème (admis) : Si un triangle est équilatéral, alors la médiane, la
hauteur , la bissectrice issues d’un même sommet, et la médiatrice du côté
opposé à ce sommet sont des droites confondues.
B
C
A
sommet
principal
base