2niv2géométrie chap3

Mathématiques 2e Niv.1 et 2 Troisième partie : Géométrie Théorie chapitre 3
COLLEGE SISMONDI (S.Z +G.E) 2012 - 2013 CH. 3, P.11
CHAPITRE 3 :
DROITES
§ 3.1 Condition d'alignement de trois points et pente de la droite
passant par deux points donnés.
Soit A = (xA; yA ), B = (B ; yB ) et C = (xC; yC ) trois points alignés (non situés sur une même verticale ).
On peut écrire, selon le théorème de Thales :
xB−xA
xC−xA
=
yB−yA
yC−yA
⇔
yB−yA
xB−xA
=yC−yA
xC−xA
Réciproquement, on peut démontrer que, si ces deux rapports sont égaux, alors les trois points sont
alignés.
On admet donc que l'équivalence suivante est toujours vraie, à savoir :
yB−yA
xB−xA
=yC−yA
xC−xA
⇔ A et B et C sont alignés.
elle est donc la condition d'alignement de deux points.
Remarque
Si deux points A et B sont situés sur une même verticale, alors ils ont la même première coordonnée :
xA = xB et la différence (xB – xA) vaut zéro.
De la même façon, si deux points A et B sont sur une même horizontale, alors yB – yA = 0.
C'est pour ces raisons que l'on a précisé que les points A, B et C ne devaient pas être sur une même
verticale ni sur une même horizontale, car les dénominateurs des fractions obtenus devaient être
différents de zéro.
Cependant, la formule obtenue finalement est valable pour des points situés sur une horizontale.

Mathématiques 2e Niv.1 et 2 Troisième partie : Géométrie Théorie chapitre 3
COLLEGE SISMONDI (S.Z +G.E) 2012 - 2013 CH. 3, P.12
Exemple :
Soit les points A = ( -4 ; -4 ), B = ( -2 ; -4 ), C = (- 2 ; -1 ), D = (- 2 ; 4 ), E = ( 1 ; 3 )
et F = ( 2 ; 5 ).
Les points A, C et F sont alignés, car
yC−yA
xC−xA
=
−1+4
−2+4
=
€
3
2
et
yF−yA
xF−xA
=
5+4
2+4
=
€
9
6
=
€
3
2
mais les points A, C et E ne sont pas alignés, car
yC−yA
xC−xA
=
€
−1+4
−2+4
=
€
3
2
et
yE−yA
xE−xA
=
3+4
1+4
=
€
7
5
De plus, on remarque que xB = xC = xD, donc les points B, C et D sont alignés verticalement.
Le rapport m =
€
yB−yA
xB−xA
est le même pour tous les points situés sur la droite passant par A et B et il
correspond bien au rapport :
€
dis tance verticale
dis tance horizontale
m=yB−yA
xB−xA
pente de la droite AB
Exemple :
Soit A = (-1; -4) et B = (-5; 6) . La pente de la droite AB , est m =
6−(−4)
−5−(−1)
=
€
10
−4
= -
€
5
2
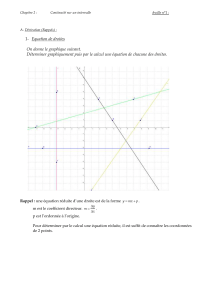
§ 3.2 Equation de la droite passant par deux points.
Soit les deux points A = ( xA; yA ) et B = ( xB ; yB ) ( non situés sur la même verticale )
et soit P = ( x ; y ) un point variable appartenant à la droite AB et distinct de A et de B.
Le point P est aligné avec A et B; ses coordonnées satisfont alors à la condition d'alignement de trois
points :
yB−yA
xB−xA
=
y−yA
x−xA
y
x
0 1
1
• •
•
•
•
•
AB
C
D
E
F

Mathématiques 2e Niv.1 et 2 Troisième partie : Géométrie Théorie chapitre 3
COLLEGE SISMONDI (S.Z +G.E) 2012 - 2013 CH. 3, P.13
La droite passant par A et B, que nous noterons dAB, est donc l'ensemble de tous les points vérifiant la
condition ci-dessus. En utilisant une notation ensembliste, on a:
dAB = { P | P = ( x ; y ) et
yB−yA
xB−xA
=
y−yA
x−xA
}
La condition
yB−yA
xB−xA
=
y−yA
x−xA
définit complètement la droite passant par A et B ; on l'appelle la condition
caractéristique (de la droite AB) et on note, de façon abusive mais bien pratique,
dAB :
yB−yA
xB−xA
=
y−yA
x−xA
Equation de la droite passant par A et B (*)
ce qui signifie que la droite AB est définie par la condition
yB−yA
xB−xA
=
y−yA
x−xA
Exemples :
1. Si A = ( 2 ; 5 ) et B = ( 3 ; -4 ), alors dAB :
−4−5
3−2
=
y−5
x−2
€
−9
1
=
€
y−5
x−2
-9(x – 2) = y – 5
-9x + 18 = y – 5
-9x – y + 23 = 0
et finalement dAB : 9x + y – 23 = 0.
Tous les points dont les coordonnées vérifient l'équation 9x + y – 23 = 0 appartiennent à la droite
dAB; par exemple, le point C = ( 1 ; 14 ) est un point de cette droite, car
9xC + yC – 23 = 9·1 + 14 – 23 = 9 + 14 – 23 = 0
mais le point D = ( 4 ; -10 ) n'appartient pas à cette droite, car
9xD + yD – 23 = 9·4 + (-10) – 23 = 36 – 33 = 3 ≠ 0.
On vérifie facilement que A et B sont bien des points de la droite passant par A et B :
9xA + yA – 23 = 9·2 + 5 – 23 = 18 + 5 – 23 = 0, donc A ∈ dAB
9xB + yB – 23 = 9·3 + (-4) – 23 = 27 – 4 – 23 = 0, donc B ∈ dAB.
2. Si A = (a; 0) et B = (0; b) sont les points d'intersection avec les axes, on a alors :
b−0
0−a
=
y−0
x−a
⇔ b(x - a) = - ay ⇔ bx + ay = ab ⇔
x
a+y b=1
Remarque :
Si les points A et B sont situés sur une même verticale, alors ils ont la même première coordonnée,
c'est-à-dire xA = xB, et tous les points de la droite passant par A et B doivent avoir la même première
coordonnée ; dAB est donc définie par x = xA.
Exemple :
La droite d, passant par ( 3 ; 5 ) et ( 3 ; -4 ) est définie par d : x = 3 ou par d : x – 3 = 0.

Mathématiques 2e Niv.1 et 2 Troisième partie : Géométrie Théorie chapitre 3
COLLEGE SISMONDI (S.Z +G.E) 2012 - 2013 CH. 3, P.14
§ 3.3. Equation de la droite passant par un point et de pente donnée.
On peut transformer l'équation (*) ainsi :
y - yA =
yB−yA
xB−xA
.
(x−xA)
et puisque
yB−yA
xB−xA
= m, on peut écrire :
y - yA = m (x - xA) Equation de la droite passant par A et de pente m
ou encore y = m.( x - xA ) + yA
y = mx + yA - m. xA
y = mx + n
y = mx + n Equation de la droite de pente m et d'ordonnée à l'origine n
Cette droite coupe l'axe des y (ensemble
des points ayant l'abscisse nulle) au
point (0; n);
par conséquent, n représente la mesure
algébrique du segment qui va
de (0; 0) à (0; n).
Exemples:
1. Déterminer l'équation de la droite passant par A = (-10; 20) et de pente
€
3
4
:
€
y−20
x−(−10)
=
€
3
4
⇔ 4y - 80 = 3x + 30 ⇔ d : 3x - 4y + 110 = 0
2. Soit la droite 3x + 11y + 17 = 0 . Quelle est sa pente et son ordonnée à l'origine ?
En écrivant y = -
€
3
11
x -
€
17
11
, on trouve sa pente m = -
€
3
11
et son ordonnée à l'origine n = -
€
17
11
.
3. Déterminer l'équation de la droite d passant par A = ( 2 ; 5 ) et parallèle à la droite passant par les
points ( -1 ; 2 ) et ( 5 ; -2 )
Nous savons que ces deux droites ont la même pente (car elles sont parallèles) ; mais la pente de la
seconde est connue: m =
€
−2−2
5−(−1)
=
€
−4
6
=
€
−2
3
Donc d :
€
−2
3
=
€
y−5
x−2
⇔ -2(x – 2) = 3(y – 5) ⇔ -2x + 4 = 3y – 15 ⇔ -2x – 3y + 19 = 0
Finalement d : 2x + 3x – 19 = 0
On vérifie facilement que A appartient à d:
2xA + 3yA – 19 = 2·2 + 3·5 – 19 = 4 + 15 – 19 = 0, donc A ∈ d.

Mathématiques 2e Niv.1 et 2 Troisième partie : Géométrie Théorie chapitre 3
COLLEGE SISMONDI (S.Z +G.E) 2012 - 2013 CH. 3, P.15
§ 3.4 Quelques remarques à propos de la pente.
1. Quels que soit les points A et B choisis sur un même droite (non verticale), la valeur de la pente est
toujours la même.
2. Si deux droites (non verticales) sont parallèles ou confondues, alors elles ont la même pente et
réciproquement (Théorème de Thales).
3. La pente d'une droite verticale n'est pas définie, car dans ce cas
xB = xA et le dénominateur de la fraction
€
yA−yB
xA−xB
est nul.
4. La pente peut être positive, négative ou nulle.
Il s'agit de distinguer trois situations différentes pour une droite, c'est-à-dire une droite peut former
avec l'axe Ox un angle positif, négatif ou nul.
Pente positive
L'angle qu'une droite forme avec l'axe des x est
positif si le plus petit angle qui permet de
« rabattre » Ox sur d est parcouru en sens anti-
horaire (sens contraire aux aiguilles d'une montre,
comme en trigonométrie).
Exemple :
Soit A = (3; 4 ) et B = (5; 6) . La pente de la droite passant par A et B est : m =
6−4
5−3
= 1
[ On peut remarquer que dans ce cas l'angle que la droite AB fait avec l'axe des x mesure 45°.]
Pente négative
L'angle qu'une droite forme avec l'axe des x
est négatif si le plus petit angle qui permet de
« rabattre » Ox sur d est parcouru en sens
horaire (sens des aiguilles d'une montre,
comme en trigonométrie).
Exemple:
Soit A = (3; 4) et B = (7; -8). La pente de la droite passant par A et B est m =
−8−4
7 −3
= -3.
Pente nulle
L'angle qu'une droite forme avec l'axe des x
est nul si la droite d est parallèle à Ox ou est
confondue avec Ox.
Si l'angle est nul, c'est-à-dire la droite d est
parallèle ou superposée à Ox,
on a yA = yB et m =
€
yB−yA
xB−xA
=
€
0
xB−xA
= 0.
La pente est nulle.