Prise en compte des effets capacitifs dans - Tel Archives ouvertes

M´ ETHODES NUM´ ERIQUES ET OUTILS LOGICIELS
POUR LA PRISE EN COMPTE DES EFFETS
CAPACITIFS DANS LA MOD´ ELISATION CEM DE
DISPOSITIFS D’´ ELECTRONIQUE DE PUISSANCE
Vincent Ardon
To cite this version:
Vincent Ardon. M´ ETHODES NUM´ ERIQUES ET OUTILS LOGICIELS POUR LA PRISE EN
COMPTE DES EFFETS CAPACITIFS DANS LA MOD´ ELISATION CEM DE DISPOSITIFS
D’´ ELECTRONIQUE DE PUISSANCE. Sciences de l’ing´enieur [physics]. Institut National
Polytechnique de Grenoble - INPG, 2010. Fran¸cais. <tel-00502938>
HAL Id: tel-00502938
https://tel.archives-ouvertes.fr/tel-00502938
Submitted on 16 Jul 2010
HAL is a multi-disciplinary open access
archive for the deposit and dissemination of sci-
entific research documents, whether they are pub-
lished or not. The documents may come from
teaching and research institutions in France or
abroad, or from public or private research centers.
L’archive ouverte pluridisciplinaire HAL, est
destin´ee au d´epˆot et `a la diffusion de documents
scientifiques de niveau recherche, publi´es ou non,
´emanant des ´etablissements d’enseignement et de
recherche fran¸cais ou ´etrangers, des laboratoires
publics ou priv´es.

UNIVERSITÉ DE GRENOBLE
INSTITUT POLYTECHNIQUE DE GRENOBLE
Noattribué par la bibliothèque
THÈSE
pour obtenir le grade de
DOCTEUR DE L’Université de Grenoble
délivré par l’Institut Polytechnique de Grenoble
Spécialité : «Génie Électrique »
Préparée au Laboratoire de Génie Électrique de Grenoble et au sein de l’entreprise CEDRAT
dans le cadre de l’École Doctorale : «Électronique, Électrotechnique, Automatique
& Traitement du Signal »
présentée et soutenue publiquement
par
Vincent ARDON
le 21 juin 2010
MÉTHODES NUMÉRIQUES ET OUTILS LOGICIELS POUR LA PRISE EN
COMPTE DES EFFETS CAPACITIFS DANS LA MODÉLISATION CEM
DE DISPOSITIFS D’ÉLECTRONIQUE DE PUISSANCE
DIRECTRICE DE THÈSE : Mme. Édith CLAVEL
CO-ENCADRANTS : M. Olivier CHADEBEC, M. Yann LE FLOCH
JURY
M. Carlos SARTORI , Président
M. Flavio CANAVERO , Rapporteur
M. Alain NICOLAS , Rapporteur
Mme. Édith CLAVEL , Directrice de thèse
M. Olivier CHADEBEC , Co-encadrant
M. Yann LE FLOCH , Co-encadrant
M. James ROUDET , Examinateur
M. François DE DARAN , Examinateur

Table des matières
Table des matières 3
Remerciements 9
Introduction générale 13
i ProjetO2M....................................... 13
ii Sous-projetSP4-CEM ................................. 14
iii Objectifsdelathèse .................................. 17
iv Plandumanuscritdethèse .............................. 18
I Modélisation des interconnexions de puissance avec la méthode PEEC 21
1 Introduction....................................... 23
1.1 Rappelducontexte............................... 23
1.2 Principe de la modélisation CEM conduite et rayonnée . . . . . . . . . . . 23
1.2.1 Perturbations conduites . . . . . . . . . . . . . . . . . . . . . . . 24
1.2.2 Perturbations rayonnées . . . . . . . . . . . . . . . . . . . . . . . 24
1.2.3 Modesdecouplage.......................... 25
1.3 Caractéristiques des structures d’électronique de puissance . . . . . . . . . 25
1.4 Rappel sur les équations de Maxwell . . . . . . . . . . . . . . . . . . . . . 27
2 Choix d’une méthode de modélisation 3D des interconnexions de puissance . . . . 28
2.1 Méthodes en interaction locale (méthodes finies) . . . . . . . . . . . . . . . 29
2.2 Méthodes en interaction globale (méthodes intégrales) . . . . . . . . . . . . 29
2.2.1 Écriture intégrale du champ électrique . . . . . . . . . . . . . . . 30
2.2.2 Discrétisation spatiale et interprétation des effets résistifs, inductifs
etcapacitifs.............................. 30
2.2.3 Choix de la méthode PEEC . . . . . . . . . . . . . . . . . . . . . 31
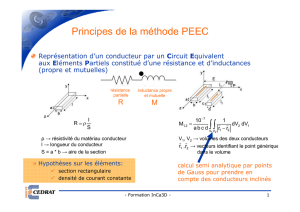
3 Présentation rapide de la méthode PEEC classique . . . . . . . . . . . . . . . . . 32
3.1 Extraction des éléments parasites à partir d’un maillage dual . . . . . . . . 32
3.2 Performances et limites de la méthode . . . . . . . . . . . . . . . . . . . . 33
4 Méthode (RLM)-PEEC adaptée aux structures basses fréquences : le logiciel InCa3D 33
3