Télécharger - Maths à Zola

3e … - …/…/20… G3 TRIGONOMETRIE
I. Problèmes
La trigonométrie est un outil pour calculer des longueurs et des mesures
d’angles dans des triangles rectangles
II. Cosinus, sinus et tangente d’un angle aigu
Un angle aigu est un angle dont la mesure est comprise entre 0° et 90°
On associe à chaque angle aigu 3 nombres particuliers appelés sinus, cosinus
et tangente de cet angle.
La calculatrice permet :
 De trouver le cosinus, le sinus et la tangente d’un angle :
 De retrouver l’angle à partir de son cosinus, de son sinus ou de sa
tangente :
III. Comment résoudre les problèmes de départ avec le cosinus, le
sinus et la tangente ?
1) Formules trigonométriques à connaître par coeur
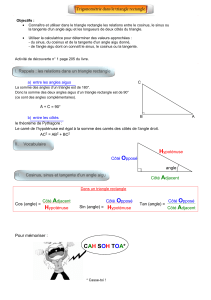
Vocabulaire :
 [AC] est l’hypoténuse 
 [BC] est le côté opposé à l’angle 
 [AB] est le côté adjacent à l’angle 
 [BC] est le côté adjacent à l’angle 
 [AB] est le côté opposé à l’angle 
Angle
30°
Cosinus de l’angle
≈ 0,87
cos
Angle
30°
Sinus de l’angle
0,5
sin
Angle
30°
Tangente de l’angle
≈ 0,58
tan
Cosinus
0,3
Angle
≈ 72,5°
SECONDE
COS
Sinus
0,6
Angle
≈ 36,9°
SECONDE
SIN
Tangente
1,2
Angle
≈ 50,2°
SECONDE
TAN

Formules trigonométriques:
Dans un triangle rectangle, on a :
 cosinus =
()
()
longueur adjacent
longueur hypoténuse
 sinus =
()
()
longueur opposé
longueur hypoténuse
 tangente =
()
()
longueur opposé
longueur adjacent
Exemple :
AB = 4cm ; BC = 3cm ; AC = 5cm
Cos 
 =
Sin 
 =
Tan 
 =
Remarque :
Le sinus et le cosinus d’un angle aigu sont toujours compris entre 0 et 1
puisque l’hypoténuse est le plus grand côté dans un triangle rectangle
Astuce : Pour se souvenir des formules, penser à « Casse toi » (CA SO TOA)
2) La trigonométrie pour calculer la mesure d’un angle
d’un triangle rectangle : résolution du problème 5
Analyse :
 On sait qu’on est dans un triangle rectangle (on peut donc penser à la
trigonométrie)
 On cherche l’angle 
 et on connaît la longueur de son côté opposé
et de son côté adjacent.
 La formule qui convient est celle de la tangente
Je précise que le triangle est
rectangle et j’écris ma formule (avec
les lettres)
Je remplace les lettres par les
mesures connues
J’utilise la calculatrice, je tape :
Shift puis tan
Je présente le résultat avec la
précision demandée
Dans le triangle ABC rectangle en C,
on a :
Donc 
Donc la valeur arrondie de
 au
degré près est 34°
3) La trigonométrie pour calculer la longueur d’un côté
d’un triangle rectangle : résolution du problème 4
Analyse :
 On sait qu’on est dans un triangle rectangle (on peut donc penser à la
trigonométrie)
 On connaît l’angle
, la longueur de l’hypoténuse et on nous
demande la longueur du côté adjacent à cet angle.
 La formule qui convient est celle du cosinus
Je précise que le triangle est
rectangle et j’écris ma formule (avec
les lettres)
Je remplace les lettres par les
mesures connues
J’utilise la calculatrice(la touche
cos)
Je présente le résultat avec la
précision demandée
Dans le triangle ABC rectangle en A,
on a :
Donc
cos42 6
AC
Donc
6 cos42AC   
Donc la valeur arrondie de AC au
millimètre près est 4,5cm

IV. Deux autres formules à retenir
Propriété 1 : 
Propriété 2 : 