TD 1 Outils pour Biologistes 2 Résultats exercices en

TD 1 Outils pour Biologistes 2
Résultats exercices en autonomie
et d’approfondissement
30BU03SV – 2016-2017
Solutions à titre indicatif. Soyez vigilant.e.s !
1 Taux métabolique et taille des animaux
Dans cet exercice nous nous proposons d’étudier la relation entre les besoins énergétiques
des animaux et leur taille.
Dans un premier temps nous proposons de revoir quelques relations géométriques sur
les surfaces et les volumes. Le besoin énergétique d’un animal va dépendre de sa masse
corporelle donc de son volume qui est relié à la taille. Vous allez explorer la relation appelée
« loi de Kleiber », qui relie les besoins énergétiques des animaux à leur taille et conclurez
sur une conséquence surprenante.
1.1 Surface, volume et taille caractéristique
a) Rappels de base. Quelles sont les dimensions physiques d’une surface et d’un volume ?
Soit un cube d’arrête de longueur L, rappelez quelle est la surface de ce cube et quel est
son volume. Rappelez les formules pour la surface et le volume d’une sphère de rayon
L. Concluez sur les puissances qui interviennent dans la dépendance du volume et de la
surface avec la longueur (arrête ou rayon) qui caractérise chacun des objets. Si pour la
sphère, vous utilisiez le diamètre plutôt que le rayon pour donner sa taille, quelles seraient
les formules pour surface et volume et comment changent les puissances ? Même question
pour le cube, si au lieu de la longueur de l’arête vous utilisiez la diagonale d’un côté.
S = Surface de dimension [S]=L2; V = Volume de dimension [V] = L3
Cube d’arrête L: S = 6L2; V = L3
Cube de diagonale Dd’une face : S = 1
2D2; V = 1
2√2D3
Volume [V] = 1
2√2L3
Sphère de rayon R: S = 4πR2.V=4π
3R3
Sphère de diamètre D: S = πD2; V = π
6D3
Les surfaces sont proportionnelles au carré de la grandeur caractéristiques, les volumes
au cube ; ce n’est pas étonnant, ça correspond aux dimensions physiques respectives
de la surface et du volume.
Quel que soit le choix de grandeur pour caractériser la taille (linéaire) de l’objet, vous
1

pouvez affirmer que la surface sera proportionnelle au carré de cette grandeur, et le
volume au cube de cette grandeur.
Ceci est vrai aussi pour des objets de forme plus « complexe » qu’un cube ou une
sphère, comme on le voit dans la question suivante.
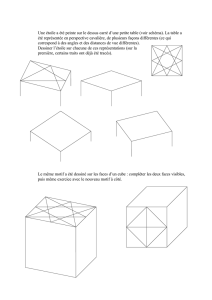
b) Soit l’objet (1) de la figure ci-dessous, composé de plusieurs cubes d’arête de longueur
L. Exprimez son volume et sa surface externe en fonction de L.
S= 18L2.V = 4L3(Dépliez la forme pour une faire un parallélépipède régulier,
comptez les « petits carrés »sur chaque face : 4*4+2 )
c) L’objet (2) de la figure est de même forme que le premier, mais « deux fois plus
grand », c’est-à-dire toutes ses dimensions sont exactement doubles de celles du premier.
Exprimez la surface et le volume du second objet en fonction de L. Les surfaces et volumes
ont-ils doublé tous les deux ?
S= 18(2L)2= 72L2;V= 4(2L)3= 32L3
Vous pouvez compter, mais passage immédiate des résultats de la forme (1) à celui
de la forme (2) par L→2Ldans l’expressions de la question (b). La surface aura
augmenté d’un facteur 22et le volume d’un facteur 23.
d) On définit une longueur dite caractéristique d’une forme, comme une longueur entre
deux points particuliers, aisément identifiables, de la forme. Pour toute forme on peut
généralement arbitrairement choisir différentes longueurs caractéristiques. Pour la forme
des objets (1) et (2) choisissons comme longueur caractéristique lcla distance entre les
faces avant et arrière. Exprimez lcen fonction de L. Quand Lest doublée, comment change
2

la longueur caractéristique lc? Comparez les longueurs caractéristiques l(1)
cet l(2) cdes deux
objets (1) et (2).
l(1)
c= 3L; si la taille caractéristique Ldouble, alors double aussi la taille caractéris-
tique l1
c, donc naturellement l(2)
c= 6L= 2l(1) c
e) Exprimez les volumes et surfaces des objets (1) et (2) en fonction de leur taille ca-
ractéristique respective. Concluez que la dépendance d’un volume ou d’une surface avec
la dimension d’un objet ne dépend pas, à un facteur numérique multiplicatif près, de la
grandeur caractéristique choisie (lc,Lou autres)
On peut raisonner géométriquement à partir de la nouvelle définition de la grandeur
chosie pour caractériser la taille : En utilisant la distance entre les faces avant et
arrières des formes (1) et (2), et en observant que la hauteur et la longueur du bloc
surélevés sont l3/3les surfaces des faces à additionner seront, pour la rangée du rangée
du bas 3×lc∗lc/3 + (2/3)lc∗lc/3 + 2(lc/3)2, pour le bloc du haut 5∗(lc/3)2, soit :
S= 18(lc/3)2= 2l2
c(Ce qui naturellement s’obtient directement par la formule de la
question b insérant lc=L/3).
Par le même raisonnement : V= 4L3= 4(lc/3)3=4
27 l3
c
Peu importe le choix de Lou de lc(ou encore d’une autre définition) pour la taille
caractéristique, la surface et le volume seront respectivement le carré et le cube de la
taille caractéristique.
f) Appliquez cette conclusion pour calculer le rapport moyen attendu entre les poids
d’un humain adulte mesurant 1 m 60 et un enfant mesurant 1 m, ainsi que le rapport des
surfaces de peau.
lA= 1,6 m , lE= 1 m. Masse adulte mA∼l3
A, masse enfant mE∼l3 E
Rapport des masses : mA
mE= (1,6 1)3'4,1
Rapport des surfaces : SA
SE= (1,6 1)2'2,6
3

1.2 Taux métabolique basal total et loi de Kleiber
On appelle taux métabolique ba-
sal (TMB) d’un animal son be-
soin énérgétique par unité de
temps minimal nécessaire pour
sa survie lorsqu’il est au re-
pos. On s’intéresse à la varia-
tion du TMB avec la taille des
animaux.
La relation dite « loi de Klei-
ber »correspond à l’observa-
tion statistique suivant laquelle
les TMBs, désignés par B,
des organismes vivants varient
comme B∼M3/4avec Mla
masse.
Sur un graphe log-log ceci
donne une relation linéaire
comme dans la figure ci-contre.
Dr. Geoffrey West, LANL (KITP Immune System Workshop 11-19-03) Scaling Laws in Biology: Growth, Mortality, Cancer and Sleep Page 3
a) En calculant log(B)en fonction de log(M), expliquer pourquoi on obtient une droite
en traçant log(B)en fonction de log(M). Quelle est la pente de la droite ?
B∼M3/4⇒log(B)∼log(M3/4) = (3/4) log(M)
b) Quel est le rapport du TMB d’un éléphant sur celui de la souris ? L’éléphant de forêt
d’Afrique Loxodonta cyclotis a une taille typique adulte de 7 m alors que la souris Mus
musculus a une taille caractéristique de 7 cm.
(Pour répondre pensez à la relation entre masse corporelle et volume et les données de
taille ci-dessus).
Comparez le résultat au simple rapport des tailles des deux animaux (autrement dit : le
TMB dépend-il linéairement de la taille typique de l’organisme ?).
Les TMB de l’éléphant et de la souris sont respectivement BE∼M3/4
Eet BS∼M3/4 S,
leur rapport est
BE
BS
=ME
MS3/4=l3
E
l3
S
3/4
Avec lEet lSles tailles de l’éléphant et de la souris.
B∼(M)3/4∼(l3
c)3/4. Le TMB varie comme la puissance 9
4de la taille.
4

c) On appelle taux métabolique basal cellulaire (TMBc) le besoin énergétique minimal
par unité de temps et par cellule d’un animal au repos (c’est-à-dire le taux métabolique
basal total divisé par le nombre de cellules dans l’organisme). En utilisant la loi de Kleiber
pour le TMB, donnez la dépendance du TMBc en fonction de la taille caractéristique L
de l’animal.
TMBc = TMB/M∼TMB/V= TMB/l3
c=l9/4
c/l3
c=l−3/4
c
d) Quel est le rapport du TMBc de l’éléphant sur celui de la souris ? Que pouvez vous
conclure sur le besoin énergétique des cellules des grands animaux par rapport à celui des
petits animaux.
TMBc = TMB/M∼TMB/V= TMB/l3
c=l9/4
c/l3
c=l−3/4
c
T MBcE
T MBcS
=l−3/4
E
l−3/4
S
= ( lS
lE
)+3/4
T MBcE
T MBcS
= (10−2)+3/4= (10−3/2)∼0,03
Le besoin énergétique par cellule des grands animaux est plus petit que celui des
anomaux plus petits !
Exercices d’approfondissement
2 Changement d’échelle
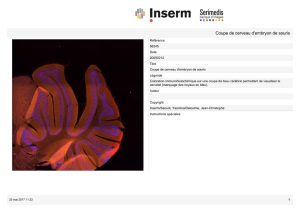
Le cerveau humain a une surface 1 000 fois plus grande
que celui de la souris. Le cerveau humain présente un
grand nombre de circonvolutions, ce qui n’est pas le
cas de la souris.
Estimez quelle est la part de l’augmentation de surface
qui s’explique uniquement par le fait que le cerveau
humain est plus grand.
Évaluez comment cette estimation est sensible à vos
approximations des dimensions des cerveaux de la sou-
ris et de l’humain ?
Rapport géométrique des surfaces : si simplement changement d’échelle la surface
varie comme la taille caractéristique au carré →rapport d’augmentation de surface
= (taille cerveau humain)2/(taille cerveau souris)2D’après l’image en considérant les
barres horizontales blanches comme l’échelle en cm on aurait :
5