Correction du bac blanc n°1

Correction du bac blanc n°1
Exercice n°1 : LE TELESCOPE HERSCHEL : Synthèse de documents
1. Expliquez brièvement l’expérience d’Herschel qui lui a permis de découvrir les infrarouges. Faire un schéma de
cette expérience.
Herschel décompose la lumière blanche du soleil avec un prisme puis utilise trois thermomètres.
Deux thermomètres mesurent la température de la pièce et un autre est placé à différents endroits du spectre.
Il s’aperçoit que la hausse de température se fait du bleu vers le rouge mais continue aussi au-delà du rouge. Il
met donc en évidence un rayonnement appelé infrarouge.
2. Quelle est le domaine de longueurs d’onde capté par le télescope Herschel ? Quelles sont les énergies
correspondantes à ce domaine ?
Le télescope Herschel détecte les longueurs d’onde : 60μm<λ <670μm
Sachant que : E=h.c/λ on a : E=6,63.10-34x 3,00.108/60.10-6=3,0.10-22J
De même : E=h.c/λ alors : E=6,63.10-34x 3,00.108/670.10-6=3,3.10-21J
Synthèse argumentée :
Le télescope Herschel, le plus grand télescope dans l’espace, a été lancé en mai 2009 par Ariane 5. Il comporte
un spectrophotomètre et deux caméras sensibles dans le domaine des ondes infrarouges et submillimétriques
(doc 4).
Ce télescope a pour mission l’observation de l’Univers dans le domaine des ondes infrarouges et
submillimétriques.
Pour cela, on utilisera ses fonctionnalités suivant deux axes (doc 4) :
L’analyse des informations de proximité, notamment lors de l’examen des nuages moléculaires comportant de
nombreuses étoiles jeunes.
L’analyse d’informations plus lointaines lors de la cartographie de la voute céleste.
Pour détecter les radiations infrarouges et submillimétriques, celles-ci doivent atteindre le détecteur
spécifique qui se trouve dans le télescope.
Cependant, d’après le document 3, ces radiations sont absorbées par l’atmosphère terrestre.
Afin d’éviter ce phénomène d’absorption, le télescope doit se situer dans l’espace.
Les poussières interstellaires (solides froids) sont chauffées par leur environnement et émettent de l’énergie
dans les domaines spectraux cités précédemment (doc.6).
Le télescope Herschel, grâce à ses capteurs de rayonnement IR maintenus à basse température et sa position
lointaine de la Terre, permet de détecter ces poussières interstellaires, leur température et les endroits où
naissent les étoiles. Herschel sondera aussi l’Univers pour détecter d’autres galaxies lointaines à l’époque de leur
formation.
Les données recueillis devraient donc nous renseigner sur la formation des étoiles, l’évolution de la vie des
galaxies et cela dans le but de mieux comprendre l’origine et l’évolution de l’Univers.

Exercice n°2 :
I.1. Les formules semi-développées des amines isomères sont :
2. Nom de l'amine B : 3-méthylbutan-1-amine
3. Au-delà de σ = 3000 cm–1 :
- le spectre 1 présente deux bandes d'absorption vers 3300 et 3400 cm–1 caractéristiques des liaisons N-H des
amines primaires. Il s’agit de la molécule B.
- le spectre 2 présente une bande d'absorption centrée sur 3300cm–1 caractéristique des liaisons N-H des
amines secondaires. Il s’agit de la molécule A.
4. On observerait aucun pic au car il n'y a pas de liaison N-H dans une amine tertiaire, donc pas de mode de
vibration associée.
5.
II.
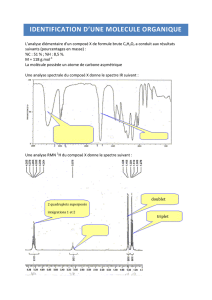
2. Spectre A : On observe :
Une bande vers 3000 cm–1 caractéristique des liaisons Ctet-H
Une bande vers 1750 cm–1 caractéristique des liaisons C=O d’un ester
Une bande vers 1250 cm–1 des liaisons C–O d’un ester
La molécule A est l'ester
Spectre B : Une bande vers 3000 cm–1 caractéristique des liaisons Ctet-H
Une bande large entre 2700-3200 cm–1 caractéristiques des liaisons O–H des acides carboxyliques
(chevauchement des bandes dues aux liaisons O-H et Ctet-H )
Une bande vers 1730 cm–1 des liaisons C=O.
Par conséquent : B est l'acide carboxylique
Spectre C : Une bande large vers 3300 cm–1 des liaisons O–Hliée d’un alcool
La molécule C est donc l’alcool.
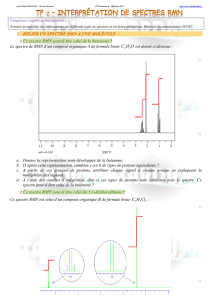
3. L'ester possède 5 groupes de protons équivalents nommés HA- HB- HC- HD- HE sur la molécule suivante :
H3(A)C-COO-CH2(B)-CH2(C)-CH(D)-(CH3(E))2
4. Pour analyse le spectre de RMN, on établit le tableau suivant :

On remarque que l'intégration est bien en accord avec le nombre de protons équivalents de chaque groupe.
Ce spectre correspond bien à la molécule d’éthanoate de 3-méthylbutyle.
5. L'acide éthanoïque possède 2 groupes de protons équivalents alors que le spectre RMN fait apparaître 3
signaux donc trois groupes de protons équivalents. Le spectre RMN n°2 n'est pas celui de l'acide éthanoïque.
6. Hauteur totale des paliers : H = 30 mm pour 6 protons présents dans cette molécule
Par conséquent 1 proton correspond à une hauteur de palier de 5 mm
Pour le 1er palier (gauche) : h1= 5mm ↔ 1 proton
Pour le 2ème palier (milieu) : h2= 10mm ↔ 2 protons
Pour le 3ème palier (droite) : h3= 15mm ↔ 3 protons
Le singulet pour δ = 6 ppm d’intégration 1 correspond à un proton n’ayant aucun voisin. Cela laisse envisager le
motif COOH
Le quadruplet pour δ = 2,9 ppm d’intégration 2 correspond à deux protons équivalents ayant trois voisins. Cela
laisse envisager le motif CH2–CH3
 (ppm)
Nature du
signal
Nombre de
H
équivalents
Nombre de
voisins
Motif envisagé
1
doublet
6 H(E)
1
CH(D)-(CH3(E))2
1,5
quadruplet
2 H(C)
2 H(B) + 1 H(D)
CH2(B)-CH2(C)-CH(D)
1,7
nonuplet
1 H(D)
6 H(E) + 2 H(C)
CH2(C)-CH(D)-(CH3(E))2
2,1
singulet
3 H(A)
0
H3(A)C-COO
4,1
triplet
2 H(B)
2 H(C)
CH2(B)-CH2(C)

Le triplet pour δ = 1,5 ppm d’intégration 3 correspond à trois protons ayant deux voisins. Cela laisse envisager le
motif est associé aux protons de CH2–CH3.
Ce spectre correspond bien à la molécule d’acide propanoïque.
Exercice 3 : QUAND LES ASTROPHYSICIENS VOIENT ROUGE…
A. L’EFFET DOPPLER
Relations à éliminer :
Relation 1 et 2 : v étant inférieure à c, les relations donnent λ < λ0 ce qui n'est pas le cas lorsque la source
s'éloigne.
Relation 3 : la relation n'est pas homogène à une distance, elle ne correspond donc pas.
La relation 4 convient car elle est bien homogène à une distance et reste cohérente avec le phénomène observé.
B. DÉTERMINATION DE LA VITESSE D’UNE GALAXIE
1. Raies de Balmer de l'atome d'hydrogène
a. Par lecture graphique on a :
Sur Terre : (H) = 656 nm ; (H) = 486 nm ;(H) = 434 nm
Pour la galaxie (H) = 683 nm ;(H) = 507 nm ; (H) = 451 nm
Ces raies font parties du spectre visible (comprises entre 400 et 800nm).
2. Choix du modèle d’étude
3. Décalage vers le rouge
a. On constate que : λ > λ0 . Cela justifie le décalage de chaque raie vers les grandes longueurs d'onde donc vers
le rouge.
b. Décalage spectral :
c. La meilleure estimation de z pour la galaxie TGS153Z170 est la moyenne des 3 valeurs obtenues : 0,0412
d.
e. Soit : v = c z

D’où : v = 3,00.108  0,0412 = 1,24  107 m.s-1
Cette valeur, calculée à partir d’une moyenne effectuée sur 3 mesures, est plus précise que la précédente
calculée à l’aide d’une seule raie.
C. DÉTERMINATION DE LA DISTANCE D’UNE GALAXIE
D. COMPARAISON DES SPECTRES DE DEUX GALAXIES
1. Le spectre du document 3 représente un spectre d'absorption puisque les raies pointent vers le bas (le
document 3 est un spectre d’émission).
2. Pour TGS153Z170, (H) = 507 nm
Pour l’autre galaxie TGS912Z356, on lit sur doc 4 : (H) = 543 nm
Par conséquent, le décalage vers le rouge est le plus important pour la TGS912Z356, donc z est aussi plus
important.
Or : 𝑧=𝑣
𝑐, donc sa vitesse
v est plus grande.
De plus, d = v / H , elle est donc plus éloignée de la Terre.
3a. L'image d'une étoile ponctuelle n'est pas ponctuelle à cause de la diffraction des rayons lumineux par
l'ouverture du télescope.
b. L'intérêt de se procurer une lunette astronomique de diamètre plus important est de réduire le phénomène
de diffraction : celui-ci est d'autant plus marqué que l'ouverture est faible. De plus, un diamètre plus important
permet de collecter d'avantage de lumière et donc d'observer des objets moins lumineux et donc plus éloignés.
Exercice n°2 - Partie A :
1. Analyse de la note la4 d’une flûte à bec
1.1. On détermine la durée t de n périodes (avec n le plus grand possible), ainsi on peut exprimer la période
T =
t
n
puis la fréquence f =
1
T
=
nt
.
Avec
t
= (10,1-1,0) = 9,1 ms pour 8 périodes T
Exemple : f =
3
8
(10,1 1,0) 10
= 8,8102 Hz
1.2. Les fréquences des harmoniques sont des multiples de celle du fondamental : fk = kxf1
Ainsi : pour l’harmonique de rang 2 : f2 = 2.f,
Soit : f2 = 1,8103 Hz.
De même, l’harmonique de rang 3 : f3 = 3.f
Soit f3 = 2,6103 Hz.
8T