Le 03-05-16 Brevet blanc

1
COLLEGE MADELEINE DANIELOU
Mardi 3 mai 2016
Brevet Blanc de Mathématiques
Durée de l’épreuve : 2 heures
L’utilisation de la calculatrice est autorisée
Le sujet comporte 7 exercices et une feuille annexe que vous devez compléter et rendre avec votre copie.
Barème donné à titre indicatif
Exercice 1 6 points
Exercice 2 5 points
Exercice 3 3 points
Exercice 4 4 points
Exercice 5 7 points
Exercice 6 6 points
Exercice 7 5 points
Rédaction et présentation 4 points

2
EXERCICE 1
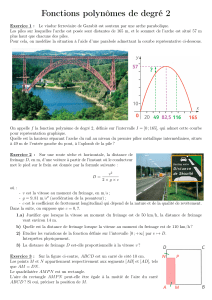
La distance parcourue par un véhicule entre le moment où le conducteur voit un obstacle et l’arrêt complet du véhicule est
schématisée ci-dessous.
1. Un scooter roulant à 45 km/h freine en urgence pour éviter un obstacle. A cette vitesse, la distance de réaction est
égale à 12,5 m et la distance de freinage à 10 m. Quelle est la distance d’arrêt ?
2. On appelle x la vitesse (en km/h) d’un véhicule sur route sèche. Soit f la fonction qui, à x, associe la distance de
réaction en mètres et g la fonction qui, à x, associe la distance de freinage en mètres. On donne la représentation
graphique de la fonction g en annexe. L’expression de la fonction f est   
.
Tracer la représentation graphique de la fonction f dans le repère donné en annexe.
3. En utilisant les deux graphiques, répondre aux questions suivantes :
a. La distance de réaction est de 15 m. A quelle vitesse roule-t-on ?
b. La distance de freinage du conducteur est-elle proportionnelle à la vitesse de son véhicule ?
Justifier votre réponse.
c. Déterminer la distance d’arrêt pour une voiture roulant à 90 km/h.
4. La distance de freinage d en mètres, d’un véhicule sur route mouillée, peut se calculer à l’aide de la formule
suivante, où v est la vitesse en km/h du véhicule :
,
Calculer la vitesse d’un véhicule en km/h (arrondie à l’unité) si la distance de freinage sur route mouillée est 79,4 m.
EXERCICE 2
Dans les marais salants, le sel récolté est stocké sur une
surface plane. On admet qu’un tas de sel a toujours la
forme d’un cône de révolution.
1. a. Pascal souhaite déterminer la hauteur d’un cône de
sel de diamètre 5 mètres. Il possède un bâton de
longueur un mètre ; il effectue des mesures et
réalise les deux schémas ci-contre.
Quelle est la hauteur de ce cône de sel ?
b. Déterminer en mètres cube le volume de sel
contenu dans ce cône. Arrondir le résultat au mètre
cube près.
2. Le sel est ensuite stocké dans un entrepôt sous forme de cônes de volume 1000 m3. Par mesure de sécurité, la hauteur
d’un tel cône de sel doit être égale à 6 mètres. Quel rayon faut-il prévoir alors pour la base ? Arrondir le résultat au
décimètre près.

3
EXERCICE 3
A la fin d’une fête de village, tous les enfants présents se partagent équitablement les 397 ballons de baudruche qui ont
servi à la décoration. Il reste alors 37 ballons.
L’année suivante, les mêmes enfants se partagent équitablement aussi les 598 ballons utilisés cette année-là. Il en reste
13.
Combien d’enfants, au maximum, étaient présents ?
Toute trace de recherche, même incomplète, sera prise en compte dans la notation.
EXERCICE 4
On s’intéresse à la zone au sol qui est éclairée par deux
sources de lumière : le lampadaire de la rue et le spot fixé en F
sur la façade de l’immeuble.
On réalise le croquis ci-contre qui n’est pas à l’échelle, pour
modéliser la situation.
On dispose des données suivantes :
PC = 5,5 m ; CF = 5 m ; HP = 4 m ;
MFC
 33° et PHL
 40°
1. Calculer la longueur PL. On arrondira la réponse au décimètre.
2. Calculer la longueur LM correspondant à la zone éclairée par les deux sources de lumière. On arrondira la réponse au
décimètre.
3. On effectue des réglages du spot situé en F afin que M et L soient confondus. Déterminer la mesure de l’angle CFM
 .
On arrondira la réponse au degré.
EXERCICE 5
Voici les caractéristiques d’une piscine qui doit être rénovée.
Document 1 : Informations sur la piscine
Vue aérienne de la piscine
Document 2 : Information relative à la pompe de
vidange.
Débit : 14 m3/h
Document 3 : Informations sur la peinture résine
utilisée pour la rénovation
 seau de 3 litres
 un litre recouvre une surface de 6 m2
 2 couches nécessaires
 Prix du seau : 69,99€
Forme : pavé droit
Profondeur : 1,2 m
1. Le propriétaire commence par vider la piscine avec la pompe de vidange. Cette piscine est remplie à ras bord.
Sera-t-elle vide en moins de 4 heures ?
2. Il repeint ensuite toute la surface intérieure de cette piscine avec de la peinture résine.
Quel est le coût de la rénovation ?
4 m
10 m

4
EXERCICE 6
Soient les fonctions f, g et h définies par :
 6  3 9  7  5  7
A l’aide d’un tableur, Elsa a construit un tableau de valeurs de ces fonctions. Elle a étiré vers la droite les formules
qu’elle avait saisies dans les cellules B2, B3 et B4.
1. Utiliser le tableur pour déterminer la valeur de 2.
2. Ecrire les calculs montrant que 3 47.
3. Faire une phrase avec le mot « antécédent » ou le mot « image » pour traduire l’égalité 3 47.
4. Quelle formule Pauline a-t-elle saisie dans la cellule B4 ?
5. a. Déduire du tableau ci-dessus une solution de l’équation 3 9  7  5  7.
b. Cette équation a-t-elle une autre solution que celle trouvée grâce au tableur ? Justifier la réponse.
EXERCICE 7
Pour chaque question une seule réponse est possible
Recopier sur votre copie le numéro de la question et les réponses A, B ou C que vous avez choisies. Aucune justification
n’est demandée mais une mauvaise réponse enlève 0,5 point.
Questions Réponse A Réponse B Réponse C
1 L’écriture en notation scientifique du nombre
587
000
000
est :
5
,
87
10
587
10
5
,
87
10
2 Si on développe puis on réduit l’expression
2
3
1
,
on obtient :
3
²
5
2
3
²
6
2
3
²
1
3 Le nombre
3
2
√
5
est égal à :
19
12
√
5
9
16
√
5
29
12
√
5
4 Le nombre
√
162
3
√
72
√
18
est égal à :
9
√
2
18
√
2
3
√
2
6
6
√
6
2
√
3
24
√
2
5
Une
vitesse
égale
à
36
km
/
h
correspond à :
360
m
/
s
60
m
/
s
10
m
/
s
6
Pierre va à vélo au collège, il part à 6 h 38. Son
trajet dure 25 minutes.
Les cours commencent à 7h05.
Il arrivera :
Exactement à l’heure En avance En retard
7 Dans un parking, il y a des motos et des voitures.
On compte 28 véhicules et 80 roues. Il y a donc :
20 voitures 16 voitures 12 voitures
8 Le produit de 18 facteurs égaux chacun à
8
s’écrit :
8
8
18
8
9
La section d’un cylindre de révolution de
diamètre 4 cm et de hauteur 10 cm par un plan
parallèle à son axe peut être :
Un rectangle
de dimensions
3 cm et 10 cm
Un rectangle
de dimensions
5 cm et 10 cm
Un rectangle
de dimensions
3 cm et 8 cm
10
Lorsque l’on regarde un angle de 18° à la loupe
de grossissement 2, on voit un angle de : 9° 36° 18°

5
3e …… NOM : ………………………………….
ANNEXE A RENDRE AVEC VOTRE COPIE
distance en mètres
vitesse en km/h
20
30
40
50
60
70
80
90
100
110
120
130
140
20
30
40
50
60
70
80
90
100
0
10
10
x
y