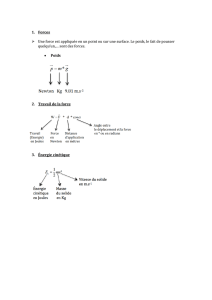
I) Voici une machine à nombre qui, lorsqu`on lui introduit un nombre

Introduction de la notion de fonction
I) Voici une machine à nombres qui, lorsqu’on lui introduit un nombre,lui associe un unique
nombre.
1) Quels sont les nombres obtenus lorsque l’on entre, dans cette machine, les nombres 60, 80 et 120.
2) Exprimer le nombre obtenu en fonction du nombre entré x.
3) L’expression f : x  0,005 x² (se lit : « la fonction f qui à x associe 0,005 x² »).
Ou f(x) = 0,005x² (se lit : « f de x égale 0,005x² »)
II) Sur route sèche la distance de freinage d d’un véhicule s’exprime en fonction de la
vitesse v par la formule suivante : d = 0,005 v² où d est exprimée en m et la vitesse v en
km.h-1.
1) Compléter le tableau suivant à l’aide d’un tableur :
v
0
10
20
30
40
50
60
70
80
90
100
110
120
130
d
D:\Mes documents\Stage 3° (1).xls
2) Dans un repère du plan représenter la distance d en fonction de la variable v. On utilisera un tableur
ou on prendra en 1 cm pour 10 km.h-1 en abscisse et 1 cm pour 10 m en ordonnée.
D:\Mes documents\Stage 3° (2).xls
3) Par lecture graphique déterminer :
_ la distance de freinage d’un véhicule roulant à 65 km.h-1.
_ la vitesse du véhicule dont la distance de freinage de freinage est de 55 m.
D:\Mes documents\Stage 3°(3).xls
On note d la fonction définie par :d(v) = 0,005 v² compléter les phrases suivantes :
_ l’image de 65 par la fonction d est …
_ l’antécédent de 55 par la fonction d est …
Entrer un
nombre
Elever au
carré
Multiplier
par 0,005
Nombre
obtenu