Dipôles en régime sinusoïdal - Site de la section STI GE du lycée

Lycée Paul Langevin Première génie électronique M. GOLAIN
Feuille d’exercices : Dipôles en régime sinusoïdal
Exercice n°1 :
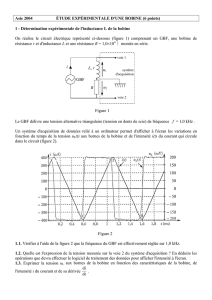
Une résistance de 1000 Ω et une bobine d’inductance 0,5 H sont placées en série et soumises à une
tension sinusoïdale de fréquence 500 Hz. A l’aide d’un voltmètre RMS en position AC+DC, on
mesure une tension aux bornes de la bobine de 10 V.
1) Donner la valeur efficace de la tension aux bornes de la bobine.
2) Exprimer, puis calculer, le module de l’impédance complexe de la bobine.
3) Quelle est la valeur efficace du courant dans le circuit ?
4) En déduire la valeur efficace de la tension aux bornes de la résistance.
5) Ecrire l’impédance complexe équivalente. En déduire l’expression de son module puis calculer sa
valeur.
6) Trouver la valeur efficace de la tension d’alimentation.
7) Quel est le déphasage du courant dans le circuit par rapport à la tension d’alimentation ?
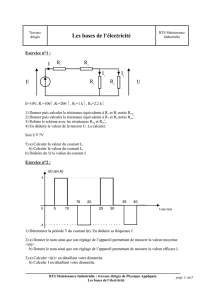
Exercice n°2 : Une résistance R = 47 Ω et une bobine d’inductance L sont placées en série et
alimentées par une tension sinusoïdale u. Un oscilloscope, branché comme l’indique le montage, a
permis de faire les relevés suivants :
1) À partir des oscillogrammes, déterminer :
a) la période, la fréquence et la pulsation de u(t) ;
b) les valeurs maximales des 2 tensions ainsi que leurs valeurs efficaces ;
c) le déphasage de u
R
par rapport à u.
2) Calculer la valeur efficace de l’intensité du courant dans le circuit.
3) En déduire la valeur du module de l’impédance du circuit.
4) Donner l’impédance complexe du circuit en fonction de R, L et ω, puis son module. En déduire la
valeur de L.
5) Retrouver la valeur du déphasage mesurée au 1c.
Exercice n°3 : On alimente une résistance en parallèle avec une bobine par une tension sinusoïdale
(
)
t942sin210)t(u = .
1) a) Donner U la grandeur complexe associée à u(t).
b) Donner la valeur de la pulsation de u(t). En déduire la fréquence de u(t).
2) Calculer Y l’admittance complexe équivalente à R et L en parallèle.
3) En déduire I.
4) Ecrire l’expression de i(t).
R = 50 Ω
L = 0,11 H
Exercice n°4 :
1)
Donner l’expression de l’admittance équivalente
Y
de R
2
en
parallèle avec C en fonction de R
2
, C et ω.
2) En déduire l’expression de l’impédance équivalente Z du
dipôle AB en fonction de R
1
, R
2
, C et ω.
Exercice n°5 :
Nous imposons une tension sinusoïdale u de valeur efficace 10 V et de
fréquence 1 kHz à un condensateur de capacité C = 1 µF en série avec une
résistance R = 220 Ω.
1) Donner l’expression, sous forme polaire, de la tension complexe U.
2) Calculer l’impédance complexe (en polaire) de ce circuit à la fréquence considérée.
3) En déduire l’expression de l’intensité complexe (en polaire) du courant qui le traverse.
4) En déduire la valeur efficace de l’intensité de ce courant et son déphasage par rapport à u.
5) Déterminer l’expression de la tension complexe U
R
aux bornes de la résistance en fonction de R,
C, ω et U (en polaire).
6) En déduire sa valeur efficace U
R
et son déphasage par rapport à u.
Exercice n°6 :
Soit le diviseur de tension suivant :
1) Donner l’expression de V
S
en fonction de V
e
.
2) Calculer V
S
si
(
)
t1257sin1,14)t(v
e
= avec R = 1 kΩ et C = 47 nF (en polaire).
3) Mêmes questions si on remplace le condensateur par une bobine d’inductance L = 200 mH et
que la fréquence de la tension v
e
passe à 8000 Hz.
R
C
V
S
V
e
C
R
i
u
u
R
C
R
1
R
2
A
B
L
R
i
u
200µs/Div
2V/Div
2V/Div
Temps : Voie 1 : u Voie 2 : u
R
0V
u
u
R
L
R
Voie 2
Voie 1
u
R
u
i
~