fig. 60). Nous avons vu (Compl. de Géom., 111) que toute pyram

GÉOMÉTRIE DESCRIPTIVE.
^Qn
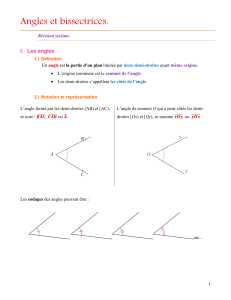
77. Inscrive une sphère dans une pyramide triangulaire
donnée [fig. 60).
Nous avons vu (Compl. de Géom., 111) que toute pyramide
triangulaire était circonscrïptible à une sphère, et qu'en menant les plans bissecteurs des angles dièdres déterminés par
la base de la pyramide proposée et ses faces latérales, on formait une nouvelle pyramide dont le sommet était précisément le centre de la sphère inscrite dans la pyramide donnée.
Ceci posé, nous admettrons pour plus de simplicité que la
base abc de cette pyramide est dans le plan horizontal. Soit
[s, s') son sommet. Menons sur le côté ab de la base la perpendiculaire sd. L'angle sdS du triangle Ssd de l'espace
mesure l'angle dièdre formé par la base avec la face latérale
Sab. Le plan bissecteur de cet angle dièdre contient la bissectrice de l'angle sdS [Compl. de Géom., 101). Prenons sur LT,
à partir de son point d'intersection a avec ss', une longueur
ad\ = «/. L'angle a-d\s' représentera l'angle sdS, et la bissectrice de l'angle ad\s sera la projection verticale de la bissectrice de l'angle sdS, lorsqu'on rend le plan de cet angle parallèle au plan vertical par une rotation autour de l'axe Ss.
En raisonnant d'une manière identique par rapport aux
perpendiculaires se et sf abaissées du point s sur les côtés bc
et ac de la base abc, on construira les angles cre\s' et <rf'ts'
qui mesurent les angles dièdres de la base avec les deux autres
faces latérales. Les bissectrices des angles ce',*' et <tf\s' seront
les projections verticales des bissectrices des angles seS et sfS,
rendus parallèles au plan vertical.
Supposons maintenant qu'on prenne un nouveau plan horizontal caractérisé par la ligne de terre L,T, parallèle à LT.
Rien ne sera changé aux projections verticales ni à la projection horizontale du triangle abc. Le nouveau plan horizontal
coupera la pyramide Mabc dont le sommet M est le centre de
la sphère inscrite dans la pyramide Sabc, suivant un triangle
c.P>y qui aura ses côtés parallèles à ceux de la base commune
abc. Il faut construire le triangle txfiy.
Si l'on prolonge les bissectrices des angles ad\s', (re\s',
af\s', jusqu'à leurs points de rencontre g\, h\, l\, avec L,T,,
et si l'on abaisse des points d\, e\, / ' , , les perpendiculaires
d\à,e\z,f\y,
sur L,T,, on obtiendra trois triangles rectangles
qui feront connaître les longueurs des projections des bissectrices des angles sdS, seS, sfS, entre les côtés des deux
triangles abc et a3y.
En effet, dans le triangle d\og\, par exemple, d',g\ est la
véritable longueur de la bissectrice de l'angle sdS entre les
deux plans horizontaux considérés, tandis que le côté d\o est
la distance de ces deux plans ou la différence de hauteur des