Quelques commentaires qui peuvent vous être

Quelques commentaires qui peuvent vous être utiles…
Magnétisme et induction
L’ère moderne du magnétisme a commencé vers 1820 et cette théorie n’est pas encore complète
Mais le pouvoir de la « pierre d"aimant(minerai appelé magnétite Fe3O4) » de se plaquer contre des objets en fer
est connu depuis l’antiquité.
I. Quelques points sur le champ B
On peut représenter le champ B par des lignes de champ ;B est tangent à une ligne
1.Le pôle nord de l’aiguille d’une boussole placée dans un champ magnétique indique l’orientation de
champ et cette boussole qui s’oriente permet de dire qu’il y a un effet magnétique
La plupart des aimants ont 2 pôles(comme l’aiguille),là où la force magnétique est la plus forte :le pôle nord et le
pôle sud :des pôles magnétiques identiques se repoussent et des pôles différents s’attirent :.une petite tige
aimantée s’appelle un dipôle magnétique. et on n’a jamais pu (en coupant cette tige de plus en plus petite) isoler
un seul pôle .Il n’existe pas de monopôle magnétique ou de « charges magnétiques »(contrairement à
l’électrostatique qui a la charge ponctuelle comme outil de base).
Les lignes de champ entrent par le pôle Sud et sortent par le pôle nord pour un aimant
Ex
barreau Fer à cheval Champ uniforme
2.Un aimant modifie donc l’espace qui l’entoure en créant un champ B (visible avec un boussole) mais Oersted
(en 1820) a découvert qu’un courant électrique pouvait aussi créer un effet magnétique. Il a aussi montré
qu’un aimant exerçait une action sur ce courant d’où un lien entre électricité et magnétisme
3.Il n’existe pas de loi universelle sur le magnétisme comme il en existe sur la gravitation ou l’électrostatique
d’où une difficulté à définir B. On définit B en général par les actions qu’il crée ou subit
II Les actions magnétiques
1.Force de Lorentz :force agissant sur une particule de charge q placée dans B
Pour subir une action dans B ,q doit être en mouvement à la vitesse v, fB =qv∧B(on trouve son sens avec la
règle des 3 doigts) ;cette force est ⊥v donc sa puissance est nulle et ΔEc=0 :une force magnétique ne peut pas
accélérer une particule v chargée q.
Unité de B=Tesla(un aimant ordinaire peut produire un champ environ de 10-2T)
Champ magnétique terrestre 5 10-3T ;un gros électroaimant 1,5T
Cette force est indispensable pour analyser tous les mouvements de particules dans B(cyclotron, spectrographe
de masse)
2.Forcede Laplace :force agissant sur un conducteur parcouru par un courant I placé dans B
Chaque électron libre est soumis à une action dans ce champ et la charge de l’ensemble des électrons libres par
unité de temps constitue le courant d’où
Si le champ est uniforme et le fil rectiligne de longueur L : FB =i L ∧B) B
(Si le champ B n’est pas uniforme ou l’élément non rectiligne FB =∫ i dL ∧B) B
Cas particulier :dans les exercices v ⊥B et la force s’écrit simplement F= iLB
3.Le moment de force sur une boucle de courant (=une ou plusieurs spires parcourue par I)
Pourquoi un moment ?parce que la force magnétique sur une boucle de courant (=circuit fermé) placée dans B est
nulle. ;mais l’action n’est pas nulle :la boucle pivote
S
Et le moment de force s’écrit NI S B sin θ(θest l’angle entre B et la perpendiculaire
à la boucle)
(On peut définir le « moment magnétique d"une boucle » μ= Ni S (S orienté avec n)
Avec S est l’aire de la boucle ;et N le nombre de spires

Ce moment peut s’écrire vectoriellement dans la direction de la normale à la surface NIS et alors le moment de la
force s’écrit M=μ∧B.
III Le champ B
Le calcul n’est pas au programme des olympiades mais il faut quand même connaître un peu la spire(quelque soit
sa forme)appelée boucle de courant
Elle délimite une surface par son contour orienté(règle du tire bouchon)
Il faut juste savoir que si la spire est parcourue par un courant (à priori ou induit) ,elle crée un champ B
dont le sens qui répond à la règle du tire bouchon.(et que le champ est proportionnel au nombre de spires de la
boucle)
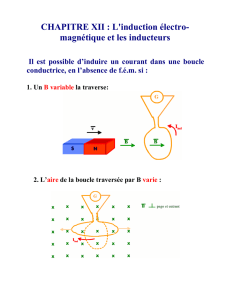
IV Induction
Il faut repérer si le conducteur soumis à l’induction peut délimiter une surface S, donc faire un contour fermé ou
une boucle de courant(carrée ou circulaire souvent)
• Savoir la définition du flux de B à travers cette surface quand le champ B est uniforme ϕ=B.S
et surtout faire en sorte que l’orientation du conducteur délimitant la surface (donc fixant le vecteur S)
fasse un flux positif(c’est à dire que S soit tel qu’il sorte du coté de B pour faire un flux positif) ;voir que le flux
est max quand S est colinéaire à B
• Ensuite appliquer la loi de Faraday e= -dϕ/dt et loi de Lenz=loi de modération :
Le courant induit a un sens tel que le champ B induit s’oppose à la variation du flux du départ
Ex :Si le flux augmente(à cause de S qui augmente ou de B ou encore de l’angle entre S et B) alors tout doit être
fait pour que ce flux diminue(par un champ B induit qui va faire diminuer le flux)Ce champ B est dû à un courant
induit dont on règle la bonne orientation pour donner le bon B induit(et ce sens est comparé à l’orientation du
conducteurr fixé au préalable)
Si le flux diminue c’est le contraire
Si le flux est sinusoïdal (parce qu’un cadre tourne avec la vitesse angulaire
ω donc ϕ=BScosθ avec θ= ωt)alors
e= -d
ϕ /dt d’où e=BS ω sin ω t
• La fem induite est équivalente à un générateur de tension instantanée qui doit être orienté comme
i(induit)d’après la convention générateur
En général ce conducteur possède une résistance R et on peut calculer i (induit) = e(induit)/R
• Dans un exo d’induction en plus d’une équation électrique (à l’instant t) liant la fem induite au circuit,
il faut en général une équation de mécanique : ce courant induit est responsable d’une action
magnétique(force ou moment de force) et il faut une équation de mouvement(ou d’équilibre éventuellement)
Cette équation de mécanique se traite différemment selon que l’on a une translation(genre tige en mouvement) ou
une rotation (genre cadre qui tourne)
Translation :ma =∑F⇒ F(laplace)+P(poids : si le mouvement est incliné ou vertical)
Ne pas oublier que le sens de la force de laplace(F =iLB avec i induit bien sur)doit modérer ce qui
est en train de se passer
Ex une tige coincée entre 2 rails ou un cadre plongés dans B que l’on tire horizontalement (à
vitesse constante donc avec un opérateur) ou verticalement (donc accéléré à cause de son poids)
Rotation : Jθ=Jdω/dt=∑M(moment de force)⇒M(moment de force magnétique =± iNSB sinθ)
C’est le théorème du moment cinétique dL/dt =J dω/dt =M(attention au signe par rapport à la
rotation choisie avec une convention positive)
Avec le moment cinétique L= moment de la quantité de mouvement =Jω
(si le moment de force est nul alors ω =constante)
Ex :Un cadre ou une spire qui tourne dans B :apparition d’un courant induit à cause de la variation du flux
(parce que le cadre tourne).Ce courant crée un moment de force qui s’oppose au déplacement donc à la rotation
et la vitesse angulaire
ω va diminuer
Remarques :le moment d’inertie vous sera donné ;tout ce que vous savez sur la translation peut être transposé à la
rotation :par ex la vitesse linéaire v→ ω ;position linéaire→position angulaire ;quantité de mouvement→moment
cinétique
• On peut utiliser d’autres théorèmes de la mécanique pour résoudre l’équation mécanique
Comme le théorème de l’énergie cinétique
Ex pour la rotation :: EC(rotation =1/2 Jω²) ; ΔEc (rot)= W (rot)=∫ Mωdt (entre A et B) =∫M dθou encore
dEc/dt =P (rot)=Mω (m moment de force magnétique)