Série 8: Enoncé

Introduction `a l’Astrophysique
S´erie 8: Enonc´e
Laboratoire d’Astrophysique http://lastro.epfl.ch
Ecole Polytechnique F´ ed´ erale de Lausanne
Semestre de printemps 2011
Exercice 1 : Nuage mol´eculaire en effondrement
Consid´ erons un mod` ele simple de cr´ eation d’une proto´ etoile par effondrement d’un
nuage mol´ eculaire en rotation.
Par la conservation du moment cin´ etique, la vitesse de rotation du nuage augmente
progressivement avec l’effondrement. La force centrip` ete r´ esultant de cette rotation fi-
nira par ´ equilibrer la gravitation, mettant fin ` a l’effondrement. La proto´ etoile aura alors
une forme de disque, dans un plan perpendiculaire ` a l’axe de rotation.
a) Nous voulons calculer le rayon “final” rfde la proto´ etoile, lorsque le nuage termi-
nera de se contracter. Partons de l’´ equation qui d´ ecrit l’´ equilibre mentionn´ e, dans
le cadre d’une trajectoire circulaire autour du centre du nuage :
ω2r=GMr
r2(1)
i. Dans cette ´ equation, nous voulons remplacer la vitesse angulaire ωpar une
fonction de la vitesse angulaire initiale ω0et d’un rayon initial r0. Exprimez
cette relation (i.e. la conservation du moment cin´ etique), en supposant que
le nuage passe d’une forme sph´ erique rigide (Is=2
5Mr2)`
a un disque rigide
(Id=1
2Mr2).
ii. Exprimez maintenant le rayon rfde la proto´ etoile en ´ equilibre, en fonction
du rayon initial, de la vitesse angulaire initiale, et de la masse totale du nuage.
b) i. Calculez la vitesse angulaire initiale ω0pour un nuage de 1 M, d’un rayon
initial de 0.5 pc et d’un rayon final de 100 UA.
ii. Quelle est la vitesse initiale de rotation (en m s−1) au bord du nuage ?
iii. Quelle est la vitesse angulaire finale du disque ? Exprimez ce dernier r´ esultat
sous forme d’une p´ eriode en ann´ ees.
iv. V´ erifiez (de tˆ ete, directement avec les bonnes unit´ es !) que cette p´ eriode est
“tr` es compatible” avec la p´ eriode obtenue par application de la troisi` eme loi
de Kepler ` a la situation...
1

S´ erie 8: Enonc´ e
Exercice 2 : Naines blanches et cosmochronologie
La fonction de luminosit´ e des naines blanches locales est un outil pr´ ecieux pour
d´ eterminer l’ˆ age de notre Galaxie. Si nous faisons l’hypoth` ese que notre Galaxie a tou-
jours exist´ e, alors nous devrions observer une fonction de luminosit´ e augmentant ind´ efiniment
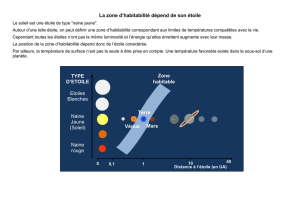
pour les ´ etoiles de faibles luminosit´ es. Nous remarquons par la figure [1] que la fonc-
tion de luminosit´ e des naines blanches s’arrˆ ete abruptement en-dessous d’une luminosit´ e
≈10−4.4L. Ceci nous indique que notre Galaxie a bien eu une p´ eriode de formation.
FIG. 1: Distribution th´ eorique et observationelle de la luminosit´ e des naines blanches.
a) A partir des mod` eles d’´ evolution stellaire, nous pouvons estimer le temps de vie
d’une ´ etoile de masse Mentre son arriv´ ee sur la s´ equence principale et la fin de
la phase de n´ ebuleuse plan´ etaire (quand la naine blanche apparaˆ ıt). L’´ equation
ci-dessous ´ evalue le temps de vie en ann´ ee τnp pour des ´ etoiles ayant une masse
0.6<(M/M)<10.
log τnp = 9.921 −3.6648 log M
M
+ 1.9697 log2M
M−0.9369 log3M M,(2)
la masse Mcorrespond ` a la masse originale de l’´ etoile sur la s´ equence principale.
Calculez le temps de vie τnp pour une ´ etoile la plus massive possible qui puisse
produire une naine blanche.
2

S´ erie 8: Enonc´ e
b) Une fois que la phase de n´ ebuleuse plan´ etaire est termin´ ee, il ne reste plus qu’un
astre chaud, tr` es dense de la taille de la Terre, c’est une naine blanche. Avec le
temps, la naine blanche va refroidir puis cristalliser. Le temps de refroidissement
τnb d’une naine blanche de masse Mnb avec une luminosit´ eLest donn´ e en ann´ ee
par :
τnb = 8.8·106A
12−1Mnb M5/7µ 2−2/7L L−5/7
(3)
o` uAle nombre de masse atomique et µle poids mol´ eculaire moyen. Nous faisons
l’hypoth` ese que nous avons une naine blanche constitu´ ee essentiellement de car-
bone (µ=A= 12) avec une masse correspondant ` a la masse moyenne d’un tel
astre, soit Mnb ≈0.6M.
Utilisez le “cut-off” de luminosit´ e de la figure [1] pour calculer le temps de refroi-
dissement τnb. Estimez alors l’ˆ age du disque galactique.
c) Estimez l’ˆ age du halo galactique en supposons qu’on observe un “cut-off” dans
la fonction de distribution des naines blanches se trouvant dans le halo, ` a une
temp´ erature effective de Teff = 4000 K (i.e. on observe des naines blanches plus
chaudes, mais pas de naines blanches plus froides). Consid´ erez pour ceci des
naines blanches de rayon terrestre (Rnb ≈10−2R) et de masse moyenne Mnb ≈
0.6M, et utilisez la loi de Stefan-Boltzmann (sans l’employer de fac¸on absolue)
avant de revenir ` a l’´ equation (3).
3