Département de physique - Phytem

1
Département de physique
PHYTEM : Exemples de composants à base de semi-conducteurs
• Rédaction du cours et travail expérimental associé : Jean-Baptiste Desmoulins (P.R.A.G.)
mail : [e-mail]
I. Isolant, conducteur, semi-conducteur .
I.1. Niveaux d'énergie dans un cristal.
Les niveaux d'énergie d'un atome isolé sont quantifiés. Au zéro absolu, les électrons restent dans les niveaux
d'énergie les plus faibles qui leurs sont permis. Pour des températures plus élevées, les électrons occupant les
niveaux d'énergie les plus élevés (ceux qui les lient le moins à l'atome) peuvent passer dans les niveaux d'énergie
encore plus élevés.
Dans un cristal, chaque atome est soumis à l'influence de ses voisins. En raison des couplages entre atomes,
les niveaux d'énergie vont se subdiviser. Le nombre de niveaux d'énergie permis va alors augmenter.
Dans un cristal, les couplages sont suffisamment forts pour que les états possibles obtenus par subdivision
soient très proches les uns des autres. L'ensemble des états qui résultent d'une subdivision peut alors être assimilé
à une bande continue. On a alors des bandes d'énergies que les électrons peuvent occuper séparées par des
bandes qui leurs sont interdites.
I.2. Distinction entre matériaux isolants et matériaux conducteurs.
I.2.1. Cas d'un solide au zéro absolu (T=0 K).
Au zéro absolu, tous les niveaux d'énergie les plus bas sont occupés. Seules les bandes d'énergie supérieures
peuvent être partiellement remplies.

2
Pour qu'il y ait conduction, il faut que l'énergie moyenne des électrons puisse varier. Ceci n'est possible que
dans le cas d'une bande partiellement remplie. On distinguera donc le cas des matériaux dont la bande de
conduction supérieure est totalement remplie qui seront dits isolants, des matériaux dont la bande supérieure est
partiellement remplie qui seront appelés conducteurs.
1.2.2. Influence de la température.
Pour une température plus élevée, l'énergie apportée par l'agitation thermique peut permettre à certains
électrons de sauter dans la bande permise supérieure, la rendant ainsi partiellement remplie et donc susceptible
de contribuer à la conduction électrique. Ce passage sera d'autant plus facile que la largeur de la bande interdite
sera plus faible.
Par exemple, cette barrière est de 1.1 eV pour le Si et 0.75 eV pour le Ge. A température ambiante, il est
possible que certains atomes de ces matériaux participent à la conduction. Ils sont alors appelés semi-
conducteurs.
En revanche, pour d'autres matériaux, la bande interdite est trop large et ils seront considérés comme isolants
à température ambiante. C'est par exemple le cas du diamant, pour lequel cette barrière est de 6 eV environ.
I.3. Les matériaux semi-conducteurs.
I.3.1. Semi-conducteur intrinsèque.
Le Si possède 4 électrons sur sa couche périphérique externe. Dans le cristal, les atomes de Si vont mettre en
commun ces électrons et se relier à leurs plus proches voisins par l'intermédiaire de 4 liaisons covalentes. Dans
l'espace, cela donne une structure tétraédrique. Dans le cas ou un atome de Si perd un électron de sa couche
externe (à cause de l'agitation thermique par exemple), cet électron peut alors participer à la conduction et on dit
qu'il y a génération de porteurs. Il apparaît alors un trou (carence d'électron), sur la couche externe de l'atome
de Si considéré. Celui-ci est alors ionisé. Inversement, si un ion de Si capte un électron et complète sa couche
périphérique externe, cette disparition de porteur est appelée recombinaison.
Une représentation simplifiée en deux dimensions de l'atome de Si au repos et ionisé est donnée sur la figure
suivante :
Néanmoins, à température ambiante, le nombre d'atomes de semi-conducteur pur (intrinsèque) susceptibles
de participer à la conduction électrique par agitation thermique est très faible (un atome sur 1013 dans le Si par
exemple ce qui représente environ une densité de porteurs de 1010 cm-3, grandeur qui augmente évidemment avec
la température). Pour être utilisé en électronique, le Si va être en général enrichi en atomes susceptibles de
contribuer à la conduction électrique. On parle alors de dopage.
1.3.2. Semi-conducteur dopé.
On ajoute, dans le cristal de semi-conducteur, des impuretés qui ont, soit un électron de valence en plus, soit
un électron de valence en moins.
Considérons l'injection d'une impureté qui apporte 5 électrons de valence. Les quatre premiers s'associent
avec les électrons de valence des atomes de Si voisins. En revanche, le cinquième est susceptible de participer à
la conduction. Chaque atome d'impureté apporte donc un électron de conduction. On parle de dopage de type N.
C'est le cas d'une injection de Phosphore (P), d'Arsenic (As) et d'Antimoine (Sb).
Dans le cas de l'injection d'atomes qui comportent trois électrons de valence, l'un des atomes de semi-
conducteur voisin ne pourra pas créer de liaison covalente. Chaque atome d'impureté apporte donc un trou. On
parle de dopage de type P. C'est le cas d'une injection de Bore (B) ou de Gallium (Ga), par exemple.

3
Usuellement, la densité d'atomes dopants reste faible devant celle des atomes de Si qui est voisine de 1023
cm-3 (exemple: 1015cm-3, 1018 cm-3…). On peut continuer à parler de Si…
Pratiquement, le dopage peut être réalisé par diffusion gazeuse (liée au fait que la concentration d'impuretés
est supérieure dans le gaz), avec par exemple du B2H6 pour un dopage P ou du PH3 pour un dopage N.
1.3.3. Mouvement des porteurs de charge.
Dans le semi-conducteur dopé, les phénomènes à prendre en compte pour représenter les mouvements des
porteurs de charge sont la diffusion, l'action d'un champ électrique, et dans le cas des récepteurs
photosensibles, les flux lumineux susceptibles de créer des porteurs de charge.
II. Jonction semi-conductrice.
C'est une structure de base qui interviendra dans bon nombre de composants à base de semi-conducteurs.
II.1. Représentation simplifiée d'une jonction semi-conductrice au repos (non polarisée).
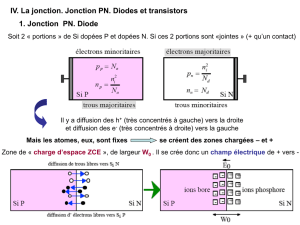
Une jonction semi-conductrice est la limite séparant un milieu dopé P d'un milieu dopé N. Dans la réalité, le
passage d'un milieu à l'autre est progressif, mais pour simplifier, nous supposerons la jonction abrupte. La mise
en contact de deux zones dopées différemment est une vue de l'esprit, mais permet néanmoins de mieux
comprendre le résultat obtenu (qui résulte dans la réalité de la diffusion d'impuretés apportées par des gaz
différents suivant les zones).
La mise en contact d'une zone dopée N (riche en électrons de conduction) avec une zone P (riche en trous) va
entraîner un processus de diffusion. Les électrons de la zone N vont diffuser vers la zone P et se recombiner. On
obtient donc des ions positifs du côté N (les atomes ont perdu un électron) et négatifs du côté P (ils ont capté un
électron supplémentaire).
La zone ionisée est appelée zone de charges d'espace ou zone de déplétion. Dans la mesure où la
concentration d'impuretés est toujours très supérieure à la densité intrinsèque d'atomes de semi-conducteur
participant à la conduction, la concentration en ions, de part et d'autre de la jonction est à peu près égale à celle
des dopants. De plus, pour simplifier, on supposera que la densité d'ions est uniforme dans chaque zone.
Le nombre d'atomes ionisés, de part et d'autre de la jonction, est identique. En revanche, la concentration de
site ionisables est différente (Nd différend de Na à priori). Par conséquent, sans autre calcul, on a
Na.Xa=Nd.Xd
De cette relation simple, il découle que la zone de charges d'espace s'étend plus du côté de moins dopé.
Sur la figure précédente, on a donc forcément Nd<Na. Il faut noter que dans la pratique, le rapport des
concentrations de part et d'autre de la jonction est souvent de l'ordre de 103. On considère donc souvent que la
largeur de la zone de charges d'espace ne dépend que du côté le moins dopé.

4
II.2. Caractéristiques de la jonction à l’équilibre.
Du côté N, on a une zone de largeur Xd uniformément chargée, avec une densité de charges +q.Nd. Du côté P,
on a une zone uniformément chargée qui a pour largeur Xa et pour densité de charge –q.Na.
• Forme du champ électrique et du potentiel.
En utilisant l'équation de Poisson, on trouve facilement le champ électrique E et le potentiel V dans chaque
zone du semi-conducteur. On appelle q la charge élémentaire et ε la permittivité du matériau (supposée identique
partout). On suppose que E = 0 à l'infini
 si x ∈ [-∞, -Xd] , on a E = 0 et on fixe V = 0
 si x ∈ [-Xd, 0] , on a E = )Xx.(
N.q d
d+
εet on fixe V = )
2
X
x.X
2
x
.(
N.q 2
d
d
2
d++
ε
−
 si x ∈ [0, Xa] , on a E = )Xx.(
Na.q a
−
ε
−et on fixe V = )
2
X
x.X
2
x
.(
N.q
V2
a
a
2
a
0+−
ε
+−
où V0 = V(-Xd)-V(Xa) = -V(Xa)
 si x ∈ [Xa, +∞] , on a E = 0 et on fixe V = - V0
Si on s'intéresse au niveau énergétique des électrons, on constate que lorsque ces derniers passent de la
région N à la région P, ils doivent franchir une marche énergétique q.V0. De même pour les trous qui passent de
la région P à la région N.
• Détermination de Vo en fonction des caractéristiques de la jonction.
Nous allons considérer les porteurs de type N. Si on s’intéresse à une zone où règne un champ électrique E(x)
et où la concentration en porteurs de type N est n(x), alors, on peut écrire qu’il existe une densité de courant de
porteurs de type N qui résulte à la fois d’un processus de conduction et d’un processus de diffusion. Dans ce cas,
on a
)x(ngrad.D.q)x(E).x(n.µ.qJ nnn
→→→ +=
Si la jonction est en circuit ouvert, alors, en régime permanent, il n’y a plus de courant moyen de porteur. Si
V représente un potentiel dont dérive le champ électrique E, µn la mobilité des porteurs de type n et Dn leur
coefficient de diffusion on peut écrire que
0
dx )x(dn
.D.q)
dx
dV
).(x(n.µ.q nn =+−
ou encore que
)x(dV.
D
µ
)x(n )x(dn
n
n
=
On intègre la relation précédente entre le côté N (ND, pno) et le côté P (npo, NA) de la jonction, ce qui donne
∫∫ =
0
o
V
n
n
po
n
D
N
dV.
D
µ
n
dn
(on tient compte directement du fait que le potentiel de la zone N est supérieur de Vo à celui de la zone P)
On peut donc déduite de cette relation que

5
)
n
N
ln(.
µ
D
Vpo
D
n
n
o=
Par ailleurs, dans un semi-conducteur, on peut écrire que T.k
G
E.q
3e.T.Kp.n −
=
où K est une constante, où T représente la température, EG l’énergie de gap à 0K et k la constante de
Boltzmann. Pour un semi-conducteur donné à une température donnée, on peut donc écrire que le produit du
nombre de porteurs de type N par celui de type P est identique que le milieu soit dopé N (ND à peu près égale au
nombre de porteurs N), dopé P (NA à peu près égale au nombre de porteurs P) ou intrinsèque (ni et pi)
ND.pno=NA.npo=ni.pi=ni2
Finalement, on a
)
n
N.N
ln(.
q
T.k
)
n
N.N
ln(.
µ
D
V2
i
DA
2
i
DA
n
n
o==
rq : la relation
p
p
n
nµ
D
µ
D
q
T.k ==
est appelée relation d’Einstein. Elle indique notamment que mobilité des porteurs et coefficient de diffusion
sont liés. Elle se démontre simplement en écrivant qu’en l’absence de polarisation, en circuit ouvert, le courant
est nul et que la densité de porteurs de type N (respectivement de type P), en dehors de la zone de charges
d’espace, est de la forme
T.k
E)x(E
c
Fc
e.N)x(n
−
−
= (respectivement T.k
E)x(E
v
Fv
e.N)x(p
−
=)
où Ec(x) (respectivement Ev(x)) est le niveau d’énergie en x des électron (respectivement des trous) et Ef le
niveau de Fermi, constant en dans le système, en l’absence de polarisation. On a en outre Ecp-Ecn=q.Vo= Evn-Evp
et Ec-Ev=EG.
rq : on aurait pu faire le même raisonnement sur les porteurs de type P.
rq : ordres de grandeur.
si on travaille à 300K, avec du Si, en prenant ND =1016 atomes/cm3, NA=1018 atomes/cm3 , et ni =1,5.1010
atomes/cm3, sachant que k = 1.38.1023 J.K-1, alors on a
mV26
q
T.k ≈ et mV820Vo
≈
• Largeur de la zone de charges d’espace.
A partir des calculs précédents concernant la largeur de la zone de déplétion du côté N et du côté P, on peut
calculer L = Xd + Xa, ce qui conduit à
0
da V).
N
1
N
1
.(
q
.2
L+
ε
=
La largeur de la zone de charges d'espace est donc proportionnelle à o
V.
II.3. Polarisation de la jonction.
Nous allons appliquer une différence de potentiel entre les deux électrodes.
Quelle que soit la polarisation de la jonction, les porteurs minoritaires, de part et d’autre de la jonction
peuvent diffuser à travers cette dernière. Il résulte de ce mouvement un courant très faible (peu de porteurs
disponibles !), appelé courant de saturation, noté Is (si ce phénomène est entretenu, c’est évidemment qu’un
système relie les parties P et N, ce qui assure le maintien des concentrations de porteurs minoritaires…). Ce
courant sera de la forme suivante :
T.k
V.q
os
o
e.II − =
Io représente le courant dans la jonction en l’absence de barrière de potentiel, q la charge élémentaire, k la
constante de Boltzmann, T la température absolue et Vo le saut de tension imposé par la jonction en l’absence de
polarisation. Ce courant ne dépend que des concentrations de porteurs au voisinage de la jonction