caracteristique d`une diode selon la temperature

Semi-conducteurs – diode en température -1
Plate-forme Matière Condensée et Cristallographie ( MCC) --- C.E.S.I.R.E. Université J.Fourier Grenoble
CARACTERISTIQUE D'UNE DIODE
SELON LA TEMPERATURE
On se propose d'étudier l'influence de la température sur une jonction PN (diode au germanium). Il s'agit
d'un monocristal unique comportant 2 régions extrinsèques en contact appelées zones P et N selon le type
d'impuretés dominant, sans discontinuité dans le réseau.
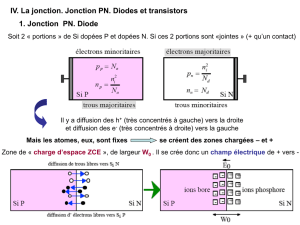
1 - La jonction PN à l'équilibre thermodynamique
L'excès d'électrons de la région N par rapport à la région P induit un mouvement de charges négatives de
la zone N (cathode) vers la zone P (anode). Un phénomène analogue se produit pour les trous qui migrent de
la zone P vers la zone N. Ainsi de part et d'autre de la jonction, apparaissent des zones de faible épaisseur (de
l'ordre du micron) où les atomes dopeurs sont progressivement ionisés, c'est à dire 2 charges d'espace, fixes
et opposées, constituant un dipôle électrique. Dans cette zone de transition existe un champ électrique interne
i
E
dirigé de la cathode vers l'anode et qui s'oppose au mouvement des électrons et des trous. Lorsque la
profondeur de la zone de transition ou zone désertée et l'intensité du champ sont suffisantes pour interdire
tout transfert des porteurs d'une zone dans l'autre, l'équilibre est atteint.
Le potentiel électrique U dont dérive i
E
a donc des valeurs différentes dans la région P et dans la
région N (UP < UN). La ddp correspondante V0 = UN - UP (quelques dixièmes de volts) est appelée
potentiel de contact ou barrière de potentiel.
D'autre part, les électrons de la région P et les trous de la région N (porteurs minoritaires) peuvent être
accélérés par le champ i
E
et traversent alors la zone désertée. Le courant correspondant Is va de N vers P.
Ce courant compense exactement le courant de recombinaison, le courant traversant la jonction en circuit
ouvert est en effet nul : Ir = Is
2. La jonction polarisée
2-1) Polarisation inverse
On relie la zone P au pôle - d'un générateur et la zone N au pôle +. La tension V1 délivrée par le
générateur s'ajoute au potentiel de contact V0, augmentant la barrière de potentiel ainsi que la largeur de la
zone désertée. L'énergie nécessaire pour franchir la barrière est alors e (V1 + V0). Or le nombre de porteurs
possédant une énergie suffisante pour franchir une barrière d'énergie EB à la température T est proportionnel
à exp[- EB
kT ] ( k = 1,38 10-23 J/K constante de Boltzmann).
Le courant de recombinaison prendra alors la valeur I1R telle que
−
−−
−
+
++
+
−
−−
−
=
==
=
kT
V
e
kT
VV
e
I
I
R
R
0
01
1
exp
exp
Seuls peuvent franchir cette
barrière les électrons de la zone N
et les trous de la zone P (porteurs
majoritaires) qui ont une énergie
d'agitation thermique supérieure à
e V0. On obtient alors un courant
Ir de P vers N appelé courant de
recombinaison car les électrons
(ou les trous) ayant franchi la
barrière se recombinent avec des
trous (ou des électrons) de l'autre
zone.

Semi-conducteurs – diode en température -2
Plate-forme Matière Condensée et Cristallographie ( MCC) --- C.E.S.I.R.E. Université J.Fourier Grenoble
ce qui entraîne I1R = IR exp[-e V1
kT ] ; V1 = UN - UP
Le courant de porteurs minoritaire I1S, quant à lui est essentiellement dû à la température et n'est donc pas
modifié par la tension V1 du moins tant que celle-ci reste assez faible pour ne pas provoquer de phénomène
d'avalanche (effet Zener). On a donc I1S = IS.
Au total la jonction est parcourue par un courant
I1 = I1R - I1S = IR exp[-e V1
kT ] - IS = IS { exp[-e V1
kT ] - 1 }
I1, négatif dans notre convention, est appelé courant inverse.
2-2) Polarisation directe
La tension V2 du générateur est appliquée dans l'autre sens et abaisse la barrière qui vaut alors V0 - V2
et diminue la zone désertée. Le courant de recombinaison augmente rapidement, le courant de porteurs
minoritaires gardant sa valeur; En première approximation on a:
I2R = IR exp[ e V2
kT ] I2S = IS
I2 = I2R - I2S = IS { exp[e V2
kT ] - 1 } V2 = UP - UN
2-3) Conclusion
Si l'on désigne par V la d.d.p. UP - UN aux bornes de la jonction, on peut décrire le courant qui la
parcourt de la zone P vers la zone N , quelque soit le signe de V par la formule:
I = IS { exp[e V
kT ] - 1 }
Cependant il faut noter la grande différence de comportement prévue par cette formule selon le signe de
V. • Pour V < 0, l'exponentielle est très vite négligeable devant l et I est pratiquement égal à la valeur -Is
quel que soit V. Ce courant de saturation est très petit par rapport au courant direct : il correspond à une
densité de courant de quelques µA/mm2.
• Pour V > 0, I augmente très vite avec la tension. Cependant pour des valeurs notables de V (quelques
Volts), les concentrations de porteurs minoritaires dans la zone désertée prenant des valeurs non
négligeables, le courant augmente moins vite que ne le prévoit la loi exponentielle et la formule ci-dessus
cesse d'être valable. Pourtant I continue de croître de façon importante avec V et le risque de destruction de
la jonction n'est pas négligeable.
3 - Variation des caractéristiques avec la température
La température modifie de façon notable les caractéristiques suivant 2 processus distincts:
a) L'agitation thermique du réseau cristallin diminue la mobilité des porteurs. C'est le phénomène
prépondérant dans les conducteurs: leur résistance augmente avec la température.
b) L'agitation thermique augmente l'énergie des électrons, ce qui leur permet de passer de la bande de
valence à la bande de conduction, ou plus facilement sur un niveau accepteur d'impureté. C'est le phénomène
le plus important dans un semi-conducteur : lorsque la température augmente, la concentration des porteurs
augmente et la résistance diminue. Ces phénomènes sont utilisés dans les applications thermométriques telles
que les sondes de température à base de diode semiconductrice à l'arséniure de gallium ou les thermistances.
Dans le cas des jonctions PN, la température intervient dans la valeur de IS d'une part et dans l'exposant
eV/kT d'autre part. On montre que, si on néglige les recombinaisons dans la zone désertée, le courant de
saturation est donné avec une bonne approximation par la relation
IS = e S ( bN + bP ) n2intrin
e = l,6.l0-19 C est la charge élémentaire, S la section de la jonction, bN et bP des quantités dépendant en
particulier des concentrations d'atomes donneurs et accepteurs respectivement dans les zones N et P, nintrin
la densité d'électrons de conduction (ou de trous) dans le semi-conducteur d'origine.

Semi-conducteurs – diode en température -3
Plate-forme Matière Condensée et Cristallographie ( MCC) --- C.E.S.I.R.E. Université J.Fourier Grenoble
On a déjà vu (TP Mesure de gap) que:
n2intrin = Ac.Av T3 exp[- Eg
kT ]
Dans ces conditions bN et bP varient peu avec la température et on a
IS = B T3 exp[- Eg
kT ]
Is augmente donc très rapidement quand T croit.
4 - Partie pratique
4.1) La température de la diode peut être évaluée grâce à une sonde de platine dont la résistance est
donnée entre 0 et 100 °C par la relation:
Rt = R0 ( 1 + A t + B t2 )
où R0 = 100 Ω t en °C
A = 3,90802.10-3 B = - 5,802.10-7
En déduire l'expression de t en fonction de R et vérifiez la fiabilité de la formule pour quelques points
entre 0 °C et 70 °C en vous reportant au tableau du classeur.
4.2) Pour tracer la caractéristique de la diode, on réalise le montage ci-dessous:
i = V1
R
V = V2 - V1
Expliquer pourquoi un montage tension-vraie ne convient pas et pourquoi le montage proposé en
intensité-vraie est plus adapté.
Relever cette caractéristique pour plusieurs valeurs de T comprises entre 10 et 60 °C.
On pourra faire varier largement U mais on s'attachera particulièrement à la zone où V varie de - 500
mV à + 50 mV qui est celle où le modèle proposé est le plus performant ( I = IS { exp[e V
kT ] - 1 } ).
Attention : il faut réduire, en inverse, l’excursion en tension lorsque la température diminue. Une valeur
de - 500 mV est acceptable à 60 °C mais ne doit pas dépasser -300 mV à 10°C.
Tracer complètement une courbe sur papier millimétré pour des valeurs de V allant jusqu'à 0.3 ~ 0.4
Volts.
Pour chacune des courbes, constituer un fichier contenant les valeurs comprises entre - 0.5 et + 0.05
Volts et déterminer à l'ordinateur par tâtonnement la valeur de Is qui fait passer la courbe calculée par les
points du fichier.
4.3) Tracer la courbe Ln ( IS
T3 ) = f ( 1
T )
En déduire le gap du germanium en joules et en électron-volts.
Pour la diode
en direct R= 1 kΩ
en inverse R= 10 kΩ