Mécanique : exercices

Mécanique :
exercices
I. Enoncé
!"
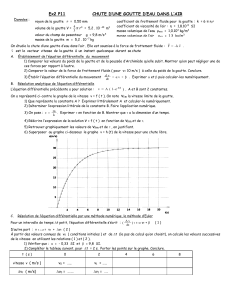
Exercice I - chute d’une goutte d’eau
• On étudie la chute d’une goutte d’eau de rayon r = 2,0 mm dans l’air,
à partir d’un nuage. On suppose sa vitesse initiale nulle. Les origine
des temps et de l’espace correspondent à l’instant et à l’endroit où la
goutte quitte le nuage à l’altitude de 1500 m.
On suppose dans un premier temps la goutte en chute libre.
1 – A partir de la deuxième loi de Newton, déterminer l’équation
horaire du mouvement de la goutte.
2 – Quelle est la valeur de la vitesse de la goutte d’eau lorsqu’elle
arrive sur le sol ? Commenter le résultat.
• La goutte est en fait soumise à une force de frottement fluide
→
f = - α.r.
→
v . La vitesse réelle de la goutte est 12 m.s
-1
lorsqu’elle
arrive au sol.
3 – Expliquer la différence entre cette valeur et celle trouvée dans la
première partie. A quoi correspond cette vitesse ?
4 – a – Calculer la valeur du poids de la goutte.
b – Calculer la valeur de la poussée d’Archimède qui s’exerce
sur la goutte. Comparer cette valeur à celle du poids.
5 – a - Etablir l’équation différentielle du mouvement.
b – En déduire l’expression de la vitesse limite du mouvement.
c – Calculer le coefficient α et le temps caractéristique τ.
Données : ρ
eau
= 1,0.10
3
kg.m
-3
; ρ
air
= 1,2 kg.m
-3
; g = 9,8 N.kg
-1
.
!"
Exercice II - saut à ski
Un skieur arrive sur le haut d’un
tremplin avec une vitesse
initiale dans le plan xOz, de
valeur
v
0
= 13 m.s
-1
et faisant un angle
θ = 30° avec l’horizontale.
On suppose que le skieur n’est soumis qu’a son poids.
1 – Quelle est la nature du mouvement du skieur ?
2 – Etablir les équations horaires du mouvement.
3 – En déduire l’équation cartésienne de sa trajectoire.
4 – Si la piste se poursuit sur l’axe Ox, déterminer la portée du saut du
skieur.
II. Corrigé
!"
Exercice I
1 – La goutte n’est soumise qu’à son poids :
m.
→
a = m.
→
g ⇔
→
a =
→
g ⇔ az = g sur un axe Oz dirigé vers le bas.
Par intégration :
vz = g.t + v0 = g.t car v0 = 0 m.s-1 (1)
z = 1
2.g.t2 + z0 = 1
2.g.t2 car z0 = 0 m. (2)
2 - La goutte atteint le sol pour z = 1500 m.
(2) ⇔ t = 2z
g
(1) ⇔ vz = g.t = g. 2z
g = 2.g.z = 2x9,8x1500 = 171 m.s-1 .
Ce résultat est beaucoup trop élevé (171 m.s-1 = 617 km.h-1).
3 – En fait, la goutte est également soumise à la force de frottement de
l’air et à la poussée d’Archimède qui s’opposent à son mouvement. 12
m.s-1 correspond à la vitesse limite, lorsque le mouvement se trouve
dans son régime asymptotique.
4 - a – P = m.g = ρeau .Vgoutte.g = 4
3.π.ρeau .r3.g
P = 4
3x3,14x(2.10-3)3x1000x9,8 = 3,3.10-4 N.
b - Π = ρair.Vgoutte.g = 4
3.π.ρair .r3.g = 4 3x3,14x(2.10-3)3x1,2x9,8
Π = 3,9.10-7 N.
On constate que Π
P ≈ 846. La poussée d’Archimède peut être
négligée devant le poids.
5 – a – On applique la deuxième loi de Newton :
m.
→
a =
→
P +
→
f ⇔ m.
→
a = m.
→
g - α.r.
→
v
En projetant sur l’axe Oz : dv
dt + αr m .v = g. (3)
b – Lorsque la force de frottement compense exactement le
poids de la goutte, la vitesse est constante et égale à la vitesse
limite : (3) ⇔ αr
m .vlim = g ⇔ vlim = mg
αr.
c - α = mg
rvlim avec m = 4
3.π.ρeau .r3 = 3,3.10-5 kg.
= 3,3.10-5x9,8
2.10-3x12 = 1,3.10-2 kg.m-1.s-1.
τ = vlim/g = 12/9,8 = 1,2 s.
!"
Exercice II
1 – Sur l’axe horizontal, le mouvement est uniforme. Sur l’axe vertical,
il est uniformément accéléré.
2 – Application de la deuxième loi de Newton :
m.
→
a = m.
→
g ⇔
→
a =
→
g puis on projette sur les axes Ox et Oz :
!
"
#
"
$
ax = 0
aZ = -g
puis par intégration :
!
"
#
"
$
vx(t) = v0.cos θ
vz(t) = - g.t + v0.sin θ (1)
on intègre à nouveau : !
"
#
"
$ x(t) = (v0.cos θ).t
z(t) = - 1
2.g.t2 + (v0.sin θ).t (2)
car x0 = z0 = 0 m.
3 – (1) ⇔ t = x
v0.cos θ
(2) ⇔ z = - g
2(v0.cos θ)2 x2 + (tan θ).x
4 – La portée correspond à l’intersection de la courbe z(x) avec l’axe
Ox, soit à z(x) = 0.
0 = - 9,8
2(13xcos 30)2 x2 + (tan 30).x , soit -3,9.10-2 x2 + 0,58.x = 0
La résolution de cette équation du second degré mène à x ≈ 15 m
La portée est donc d’environ 15 mètres.
MemoPage.com SA © / 2006 / Auteur : Emmanuel Parras