Traité d`électricité : analyse et synthèse des systèmes logiques

CHAPITRE 1
MODES DE REPRÉSENTATION
DES SYSTÈMES COMBINATOIRES
1.1 MODÈLES LOGIQUES
1.1.1 Introduction
Trois hypothèses simplificatrices permettent de décrire certains systèmes concrets
à l'aide de grandeurs dépendant du temps et n'ayant que deux états physiques distincts.
Le chapitre 1 est consacré à l'étude d'éléments dont les états de sortie dépendent unique-
ment des états d'entrée mesurés au même instant. On définit la fonction logique d'un tel
élément comme étant le tableau de correspondance entre les états d'entrée et les états de
sortie; divers modes de représentation de ces fonctions sont introduits : tables, diagram-
mes de Venn et expressions algébriques. L'algèbre logique introduite à cet effet repose
sur un nombre restreint de postulats dont il découle des théorèmes qui sont démontres
et illustrés par des applications pratiques.
1.1.2 Définition
On appelle système concret tout objet physique comportant un nombre fini d'ac-
cès ou bornes; certaines d'entre elles sont les bornes d'entrée, les autres sont les bornes
Fig. 1.1
GND = 0v

2 ANALYSE ET SYNTHÈSE DES SYSTÈMES LOGIQUES
de sortie et l'état physique des premières détermine de façon plus ou moins complexe
l'état des secondes en fonction du temps.
1.1.3 Exemple
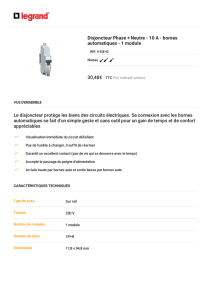
Le schéma électronique de la figure 1.1 présente un système concret comportant
deux bornes d'entrée (désignées par 1 et 2) et une borne de sortie (désignée par 3).
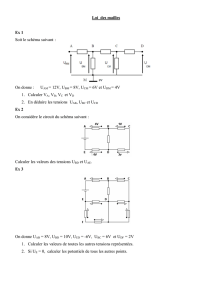
1.1.4 Expérience
La figure 1.2 décrit la variation en fonction du temps t des tensions électriques
xl(t)'x2(t) etx3(t)
mesurées entre les trois bornes du schéma de la figure 1.1 et la
terre; ce diagramme temporel ou chronogramme constitue le protocole d'une expérience.
On constate que :
• les tensions d'entrée x\ et x^ ne prennent au cours du temps que deux états
physiques distincts : 0V et +5V; ces deux états seront simplement désignés par
les symboles 0 et 1 ;
• la tension de sortie x^ varie de façon continue et prend au cours du temps une
infinité d'états physiques distincts.
• %^
x,(t) 0 ^«^
X,(t) 0 //W
V,
Y It)
va
Xi(t) —————
1
2 ————
X, (t) 0 ————
1
X(t) o
Y(t) 0 ————
Z(t) Q
Y-
AO. -
A|—
^
^
^i
A
:^^^
W/M.
A,o
A
A
/
01
/
Fig. 1.2
1.1.5 Commentaire
Pour décrire le comportement du système concret de la figure 1.1, on cherche à
établir une relation entre les variations des entrées et celles de la sortie; une telle relation
serait facilitée si la tension de sortie x3 se présentait sous la forme des tensions d'entrée

MODES DE REPRÉSENTATION DES SYSTÈMES COMBINATOIRES 3
X1 ou x2, c'est-à-dire si elle ne comportait que deux états 0 et 1. L'introduction de trois
hypothèses simplificatrices permettra d'aboutir au résultat recherché : la représentation
finale de x3 sera une traduction approximative de la réalité physique ou modèle du système
concret.
1.1.6 Première hypothèse
En admettant l'existence de deux tensions constantes VQ et v^ (fig. 1.2) on peut
déterminer à chaque instant une variable Xy(t) définie de la façon suivante :
• X3(t) = 0 si xs(t) < VQ
• Xs(t) = 1 si xs(t) > vi
• X3(t) = 2 si ro < X3(t) < v,
La variable Xy peut prendre trois valeurs distinctes ou états : X^ est un signal discret ou
quantifié; la description de ^3 par Xy est une quantification de x^.
On constate dans la figure 1.2 que l'état X^ = 2 apparaît transitoirement, lors du pas-
sage direct ou inverse des états Xy = 0 à Xy = 1 : cette constatation suggère une deuxième
hypothèse.
1.1.7 Deuxième hypothèse
En admettant que la durée des variations des entrées est nettement supérieure à la
durée de l'état transitoire caractérisé par Xy = 2, on peut négliger la représentation de
cet état : la variable X(t) (fîg. 1.2) illustre une telle simplification.
On constate alors que le signal X(t) ne comporte que deux états 0 et 1 ; on cons-
tate également l'existence de retards ou délais séparant l'action sur les entrées (variations
de x\ et x^) des effets sur la sortie (variations de X) '. on remarque en particulier que le
délai AOI lors d'une variation de A" de 0 à 1 n'est pas égal au délai Aïo de la variation
inverse.
1.1.8 Troisième hypothèse
En admettant que les délais Aoi et Aïo sont égaux à une constante A, indépendante
du temps, la variable X(t) peut être remplacée par une nouvelle variable Y(t) (fig. 1.2).
1.1.9 Définition : modèle logique asynchrone
En admettant successivement les trois hypothèses de la quantification, de l'élimi-
nation des transitoires et de l'égalisation des délais on obtient un modèle particulier du
système concret étudié : c'est le modèle logique asynchrone auquel se réfère l'ensemble
du présent volume.
1.1.10 Définition : modèle logique combinatoire
En admettant que le délai A de Y(t) est nul, on obtient la variable Z(t) (fig. 1.2)
qui décrit un cas particulier très important du modèle asynchrone : c'est le modèle lo-
gique combinatoire.